Used to hold the error state and return it to the application. More...
Classes | |
| class | Mesh |
| A Mesquite::Mesh is a collection of mesh elements which are composed of mesh vertices. Intermediate objects are not accessible through this interface (where intermediate objects include things like the faces of a hex, or an element's edges). More... | |
| class | EntityIterator |
| Iterates through a set of entities. An EntityIterator is typically obtained via Mesh::vertex_iterator() or Mesh::element_iterator(). An iterator obtained in this way iterates over the set of all vertices/elements in the Mesh from which the iterator was obtained. More... | |
| class | MeshDomain |
| class | AddQualityMetric |
| Combines two quality metrics (qMetric1 and qMetric2 defined in the parent class CompositeQualityMetric) by addition for two- and three-diminsional elements. Note: This function should not be used to combine a node-based metric with an element-based metric. More... | |
| class | ASMQualityMetric |
| Computes the ASM (Area Smoothness Metric) of the given element. More... | |
| class | AspectRatioGammaQualityMetric |
| Object for computing the aspect ratio gamma of simplicial elements. More... | |
| class | CompositeOFAdd |
| Adds two ObjectiveFunction values together. More... | |
| class | CompositeOFMultiply |
| Multiplies two ObjectiveFunction values together. More... | |
| class | CompositeOFScalarAdd |
| Adds a scalar to a given ObjectiveFunction. More... | |
| class | CompositeOFScalarMultiply |
| Scales a given an ObjectiveFunction. More... | |
| class | ShapeGuides811 |
| Shape Improvement with Unit Aspect Ratio. Use with sR-DFT. More... | |
| class | ShapeGuides812 |
| Shape Improvement with non-Unit Aspect Ratio. Use with sR-DFT. More... | |
| class | ShapeSizeGuides821 |
| Shape and Size Improvement with Unit Aspect Ratio and Equidistributed Size. Use with R-DFT. More... | |
| class | ShapeSizeGuides822 |
| Shape and Size Improvement with Unit Aspect Ratio and Preserved Size. Use with R-DFT. More... | |
| class | ShapeSizeGuides823 |
| Shape and Size Improvement with non-Unit Aspect Ratio and Equidistributed Size. Use with R-DFT. More... | |
| class | ShapeSizeGuides824 |
| Shape and Size Improvement with non-Unit Aspect Ratio and Preserved Size. Use with R-DFT. More... | |
| class | RezoneGuides832 |
| Rezone with Angle Improvement. Use with I-DFT. More... | |
| class | DeformingDomainGuides841 |
| Deforming Domain Mesh Tracking. Use with I-DFT or R-DFT. More... | |
| class | DeformingDomainGuides843 |
| Deforming Domain with Angle Improvement. Use with I-DFT or R-DFT. More... | |
| class | DeformingDomainGuides844 |
| Deforming Domain with Angle Improvement, non-Unit AR. Use with R-DFT. More... | |
| class | ConditionNumberQualityMetric |
| Computes the condition number of given element. More... | |
| class | ConjugateGradient |
| Optimizes the objective function using the Polack-Ribiere scheme. More... | |
| class | CornerJacobianQualityMetric |
| Computes the volume or area of the element, as appropriate. This metric uses the average of the corner Jacobian determinants for the approximation to the volume of hex. More... | |
| class | CornerTagHandles |
| Utility class to manage tag handles for corner tags. More... | |
| class | CornerTag |
| A class for caching and managing Tags on element corners. More... | |
| class | DistanceFromTarget |
| Base class for the computation of the distance from target between the target matrices W and the actual corner matrices A. More... | |
| class | EdgeLengthQualityMetric |
| Computes the lengths of the edges connected to given a vertex.. More... | |
| class | EdgeLengthRangeQualityMetric |
| Computes the edge length range metric for a given vertex. More... | |
| class | Exponent |
| class | FeasibleNewton |
| High Performance implementation of the Feasible Newton algorythm. More... | |
| class | FileTokenizer |
| Parse a file as space-separated tokens. More... | |
| class | GeneralizedConditionNumberQualityMetric |
| Computes the condition number of given element. The``condition number" is scaled between one and infinity, with an ideal element having condition number one. More... | |
| class | GeomTSTT |
| A base class describing a Mesquite::MeshDomain implemented on top of the TSTT geometry and classification interfaces. More... | |
| class | I_DFT |
| Class containing the target corner matrices for the context based smoothing. More... | |
| class | I_DFT_Generalized |
| I_DFT metric where mAlpha, mBeta, mGamma, and UseBarrierDelta can be set be the user. Defaults are mAlpha = .5, mBeta = 1, mGamma = 2/3. More... | |
| class | I_DFT_InverseMeanRatio |
| I_DFT metric with mAlpha = 1/3, mBeta = 0.0, mGamma = 2/3. More... | |
| class | I_DFT_NoBarrier |
| I_DFT metric with mAlpha = .5, mBeta = 1, mGamma = 0. More... | |
| class | I_DFT_StrongBarrier |
| I_DFT metric with mAlpha = .5, mBeta = 1, mGamma = 2/3. More... | |
| class | I_DFT_WeakBarrier |
| I_DFT metric with mAlpha = .5, mBeta = 1, mGamma = 2/3. More... | |
| class | IdealWeightInverseMeanRatio |
| Computes the inverse mean ratio of given element. More... | |
| class | IdealWeightMeanRatio |
| Computes the mean ratio quality metric of given element. More... | |
| class | InstructionQueue |
| An InstructionQueue object gathers Mesquite Instructions and ensures that the instruction queue is coherent for mesh improvement and/or mesh quality assessment purposes. More... | |
| class | LaplacianIQ |
| class | LaplacianSmoother |
| class | LInfTemplate |
| Computes the L_infinity objective function for a given patch, i.e., LInfTemplate::concrete_evaluate returns the maximum absolute value of the quality metric values on 'patch'. More... | |
| class | LocalSizeQualityMetric |
| Computes the local size metric for a given vertex. More... | |
| class | LPtoPTemplate |
| Calculates the L_p objective function raised to the pth power. That is, sums the p_th powers of (the absolute value of) the quality metric values. More... | |
| class | LVQDTargetCalculator |
| This is an intermediary class. Concrete classes will simply instantiate the various guide enums in their constructor. More... | |
| class | Matrix3D |
| 3*3 Matric class, row-oriented, 0-based [i][j] indexing. More... | |
| class | MaxTemplate |
| Computes the maximum quality metric value. More... | |
| class | MeanMidNodeMover |
| Class to adjust positions of higher-order nodes. More... | |
| class | MeshImpl |
| MeshImpl is a Mesquite implementation of the Mesh interface. Applications can also provide their own implementation of the interface. More... | |
| class | MeshImplData |
| Class to store mesh representation for MeshImpl. More... | |
| class | MeshImplVertIter |
| VertexIterator for MeshImpl. More... | |
| class | MeshImplElemIter |
| ElementIterator for MeshImpl. More... | |
| struct | TagDescription |
| class | MeshImplTags |
| Store tags and tag data for Mesquite's native mesh representation. More... | |
| class | MeshSet |
| The MeshSet class stores one or more Mesquite::Mesh pointers and manages access to the mesh information. More... | |
| class | MeshTransform |
| class | MeshTSTT |
| The name of the tag (integer) used internally by MeshTSTT to eliminate duplicate vertices. More... | |
| class | MsqDebug |
| Run-time activation/deactivation of debug flags. More... | |
| class | MsqError |
| Used to hold the error state and return it to the application. More... | |
| class | MsqPrintError |
| Utility class for printing error data - used in Mesquite tests. More... | |
| class | MsqFPE |
| Utility class used by InstructionQueue SIGFPE option. More... | |
| class | MsqFreeVertexIndexIterator |
| iterates over indexes of free vetices in a PatchData. More... | |
| class | MsqHessian |
| Vector3D is the object that effeciently stores the objective function Hessian each entry is a Matrix3D object (i.e. a vertex Hessian). More... | |
| class | MsqInterrupt |
| Class to watch for user-interrupt (SIGINT, ctrl-C) More... | |
| class | MsqMeshEntity |
| MsqMeshEntity is the Mesquite object that stores information about the elements in the mesh. More... | |
| class | Timer |
| class | StopWatch |
| class | StopWatchCollection |
| class | FunctionTimer |
| class | MsqVertex |
| MsqVertex is the Mesquite object that stores information about the vertices in the mesh. More... | |
| class | MultiplyQualityMetric |
| Combines two quality metrics (qMetric1 and qMetric2 defined in the parent class CompositeQualityMetric) by multiplication for two- and three-diminsional elements. Note: This function should not be used to combine a node-based metric with an element-based metric. More... | |
| struct | ActiveSet |
| class | NonSmoothSteepestDescent |
| class | NullImprover |
| class | ObjectiveFunction |
| Base class for concrete Objective Functions ObjectiveFunction contains a pointer to a QualityMetric. If the ObjectiveFunction is associated with more than one QualityMetric (i.e., the Objective is a composite, and the composed ObjectiveFunctions are associated with different QualityMetrics), then the QualityMetric pointer is set to NULL.. More... | |
| class | ParameterSet |
| class | PatchData |
| class | PatchDataVerticesMemento |
| Contains a copy of the coordinates of a PatchData. More... | |
| class | PatchDataMem |
| class | PatchDataParameters |
| class | PatchDataUser |
| This should be the parent class of all algorithms retrieving information from a MeshSet object. More... | |
| class | PlanarDomain |
| class | PowerQualityMetric |
| Raises a single quality metrics (qMetric1) to an arbitrary power (a double value, scaleAlpha) for two- and three-diminsional elements. More... | |
| class | QualityAssessor |
| A QualityAssessor instance can be inserted into an InstructionQueue to calculate and summarize registered QualityMetrics for the mesh. More... | |
| class | QualityImprover |
| Base class for all quality improvers. Mote that the PatchData settings are inherited from the PathDataUser class. More... | |
| class | QualityMetric |
| Base class for concrete quality metrics. More... | |
| class | Randomize |
| Randomly perftubs the (un-culled) vertices. More... | |
| class | RI_DFT |
| Class containing the target corner matrices for the context based smoothing. More... | |
| class | ScalarAddQualityMetric |
| Adds a number (a double) to the quality metric value. More... | |
| class | ScalarMultiplyQualityMetric |
| Multiplies quality metric value by a number (a double). More... | |
| class | ShapeImprovementWrapper |
Wrapper which performs a Feasible Newton solve using an 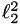 objective function template with inverse mean ratio. More... objective function template with inverse mean ratio. More... | |
| class | ShapeQualityMetric |
| class | sI_DFT |
| Class containing the target corner matrices for the context based smoothing. More... | |
| class | SmartLaplacianSmoother |
| class | SmoothnessQualityMetric |
| class | SphericalDomain |
| class | sRI_DFT |
| Class containing the target corner matrices for the context based smoothing. More... | |
| class | SteepestDescent |
| class | TargetCalculator |
| Base class that provides the interface for computing the target corner matrices used in the context based smoothing. More... | |
| class | TargetMatrix |
| Class containing the target corner matrices for the context based smoothing. More... | |
| class | TerminationCriterion |
| The TerminationCriterion class contains functionality to terminate the VertexMover's optimization. More... | |
| class | TopologyInfo |
| Information about different element topologies. More... | |
| class | TopologyModifier |
| class | UntangleBetaQualityMetric |
| The untangle beta quality metric. More... | |
| class | UntangleQualityMetric |
| class | Vector3D |
| Vector3D is the object that effeciently stores information about about three-deminsional vectors. It is also the parent class of MsqVertex. More... | |
| class | VertexConditionNumberQualityMetric |
| Computes the condition numbers of the corner's of elements connected to the given vertex and then averages those values. More... | |
| class | VertexMover |
| class | VolumeQualityMetric |
| class | WTargetCalculator |
| This is a concrete class. More... | |
| class | GeomTSTTCommon |
| Common code for specific implementations of MeshDomain on TSTT interfaces. More... | |
| class | DomainTSTT |
| class | GeomEntTSTT |
| class | TSTTIterator |
| Wrapper around single-entity TSTT interator. More... | |
| class | SIDLIterator |
| Iterate over a sidl array of TSTT entity handles. More... | |
| class | TSTTArrIter |
| TSTT iterator using array-iterator interface and buffer of handles. More... | |
| class | MeshTSTTImpl |
| Implementation of MeshTSTT. More... | |
Typedefs | |
| typedef EntityIterator | VertexIterator |
| typedef EntityIterator | ElementIterator |
| typedef void * | TagHandle |
| Type used to refer to a tag defintion. More... | |
| typedef int | StatusCode |
| typedef double | real |
| typedef void(* | msq_sig_handler_t )(int) |
Enumerations | |
| enum | DomainHint { NO_DOMAIN_HINT, PLANAR_DOMAIN, LOCAL_PALANAR, SMOOTH_DOMAIN } |
| A hint on the characteristics of the domain that Mesquite may use to determine what, if any, scheme to use to cache characteristics of the geometric domain. More... | |
| enum | StatusCodeValues { MSQ_FAILURE = 0, MSQ_SUCCESS } |
| enum | EntityTopology { POLYGON =7, TRIANGLE =8, QUADRILATERAL =9, POLYHEDRON =10, TETRAHEDRON =11, HEXAHEDRON =12, PRISM =13, PYRAMID =14, SEPTAHEDRON =15, MIXED } |
| enum | ReleaseType { STABLE_RELEASE, BETA, ALPHA } |
Functions | |
| size_t | vertices_in_topology (EntityTopology) |
| const char * | version_string (bool include_build_number=false) |
| unsigned int | major_version_number () |
| unsigned int | minor_version_number () |
| unsigned int | build_number () |
| Mesquite::ReleaseType | release_type () |
| template<class T > | |
| T | MSQ_MIN_2 (T a, T b) |
| template<class T > | |
| T | MSQ_MAX_2 (T a, T b) |
| double | cbrt (double d) |
| double | cbrt_sqr (double d) |
| double | pow (double value, const Exponent &exp) |
| bool | m_gdft_2 (double &obj, const Vector3D x[3], const Vector3D &n, const Matrix3D &invR, const Matrix3D &Q, const double alpha=0.5, const Exponent &gamma=1.0, const double delta=0.0, const double beta=0.0) |
| bool | g_gdft_2 (double &obj, Vector3D g_obj[3], const Vector3D x[3], const Vector3D &n, const Matrix3D &invR, const Matrix3D &Q, const double alpha=0.5, const Exponent &gamma=1.0, const double delta=0.0, const double beta=0.0) |
| bool | h_gdft_2 (double &obj, Vector3D g_obj[3], Matrix3D h_obj[6], const Vector3D x[3], const Vector3D &n, const Matrix3D &invR, const Matrix3D &Q, const double alpha=0.5, const Exponent &gamma=1.0, const double delta=0.0, const double beta=0.0) |
| bool | m_gdft_3 (double &obj, const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | g_gdft_3 (double &obj, Vector3D g_obj[4], const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | h_gdft_3 (double &obj, Vector3D g_obj[4], Matrix3D h_obj[10], const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | g_gdft_2_v0 (double &obj, Vector3D &g_obj, const Vector3D x[3], const Vector3D &n, const Matrix3D &invR, const Matrix3D &Q, const double alpha=0.5, const Exponent &gamma=1.0, const double delta=0.0, const double beta=0.0) |
| bool | g_gdft_2_v1 (double &obj, Vector3D &g_obj, const Vector3D x[3], const Vector3D &n, const Matrix3D &invR, const Matrix3D &Q, const double alpha=0.5, const Exponent &gamma=1.0, const double delta=0.0, const double beta=0.0) |
| bool | g_gdft_2_v2 (double &obj, Vector3D &g_obj, const Vector3D x[3], const Vector3D &n, const Matrix3D &invR, const Matrix3D &Q, const double alpha=0.5, const Exponent &gamma=1.0, const double delta=0.0, const double beta=0.0) |
| bool | h_gdft_2_v0 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[3], const Vector3D &n, const Matrix3D &invR, const Matrix3D &Q, const double alpha=0.5, const Exponent &gamma=1.0, const double delta=0.0, const double beta=0.0) |
| bool | h_gdft_2_v1 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[3], const Vector3D &n, const Matrix3D &invR, const Matrix3D &Q, const double alpha=0.5, const Exponent &gamma=1.0, const double delta=0.0, const double beta=0.0) |
| bool | h_gdft_2_v2 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[3], const Vector3D &n, const Matrix3D &invR, const Matrix3D &Q, const double alpha=0.5, const Exponent &gamma=1.0, const double delta=0.0, const double beta=0.0) |
| bool | g_gdft_3_v0 (double &obj, Vector3D &g_obj, const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | g_gdft_3_v1 (double &obj, Vector3D &g_obj, const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | g_gdft_3_v2 (double &obj, Vector3D &g_obj, const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | g_gdft_3_v3 (double &obj, Vector3D &g_obj, const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | h_gdft_3_v0 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | h_gdft_3_v1 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | h_gdft_3_v2 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| bool | h_gdft_3_v3 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[4], const Matrix3D &invR, const Matrix3D &Q, const double alpha=1.0/3.0, const Exponent &gamma=2.0/3.0, const double delta=0.0, const double beta=0.0) |
| void | centroid_smooth_mesh (PatchData &pd, size_t num_adj_vtx, msq_std::vector< size_t > adj_vtx_ind, size_t free_ind, size_t dimension, MsqError &err) |
| msq_stdio::ostream & | operator<< (msq_stdio::ostream &s, const Matrix3D &A) |
| msq_stdio::istream & | operator>> (msq_stdio::istream &s, Matrix3D &A) |
| bool | operator== (const Matrix3D &lhs, const Matrix3D &rhs) |
| bool | operator!= (const Matrix3D &lhs, const Matrix3D &rhs) |
| const Matrix3D | operator+ (const Matrix3D &A, const Matrix3D &B) |
| const Matrix3D | operator- (const Matrix3D &A, const Matrix3D &B) |
| const Matrix3D | mult_element (const Matrix3D &A, const Matrix3D &B) |
| Multiplies entry by entry. This is NOT a matrix multiplication. More... | |
| double | Frobenius_2 (const Matrix3D &A) |
| Return the square of the Frobenius norm of A, i.e. sum (diag (A' * A)) More... | |
| Matrix3D | transpose (const Matrix3D &A) |
| const Matrix3D | operator* (const Matrix3D &A, const Matrix3D &B) |
| const Matrix3D | operator* (const double &s, const Matrix3D &A) |
| friend function to allow for commutatative property of scalar mulitplication. More... | |
| int | matmult (Matrix3D &C, const Matrix3D &A, const Matrix3D &B) |
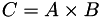 More... More... | |
| const Vector3D | operator* (const Matrix3D &A, const Vector3D &x) |
Computes 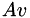 . More... . More... | |
| const Vector3D | operator* (const Vector3D &x, const Matrix3D &A) |
Computes 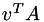 . More... . More... | |
| void | eqAx (Vector3D &v, const Matrix3D &A, const Vector3D &x) |
| void | plusEqAx (Vector3D &v, const Matrix3D &A, const Vector3D &x) |
| void | plusEqTransAx (Vector3D &v, const Matrix3D &A, const Vector3D &x) |
| void | plusEqaA (Matrix3D &B, const double a, const Matrix3D &A) |
| double | det (const Matrix3D &A) |
| void | inv (Matrix3D &Ainv, const Matrix3D &A) |
| void | timesInvA (Matrix3D &B, const Matrix3D &A) |
| void | QR (Matrix3D &Q, Matrix3D &R, const Matrix3D &A) |
| bool | m_fcn_2e (double &obj, const Vector3D x[3], const Vector3D &n, const double a, const Exponent &b, const Exponent &c) |
| bool | g_fcn_2e (double &obj, Vector3D g_obj[3], const Vector3D x[3], const Vector3D &n, const double a, const Exponent &b, const Exponent &c) |
| bool | h_fcn_2e (double &obj, Vector3D g_obj[3], Matrix3D h_obj[6], const Vector3D x[3], const Vector3D &n, const double a, const Exponent &b, const Exponent &c) |
| bool | m_fcn_2i (double &obj, const Vector3D x[3], const Vector3D &n, const double a, const Exponent &b, const Exponent &c, const Vector3D &d) |
| bool | g_fcn_2i (double &obj, Vector3D g_obj[3], const Vector3D x[3], const Vector3D &n, const double a, const Exponent &b, const Exponent &c, const Vector3D &d) |
| bool | h_fcn_2i (double &obj, Vector3D g_obj[3], Matrix3D h_obj[6], const Vector3D x[3], const Vector3D &n, const double a, const Exponent &b, const Exponent &c, const Vector3D &d) |
| bool | m_fcn_3e (double &obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | g_fcn_3e (double &obj, Vector3D g_obj[4], const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | h_fcn_3e (double &obj, Vector3D g_obj[4], Matrix3D h_obj[10], const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | g_fcn_3e_v3 (double &obj, Vector3D &g_obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | g_fcn_3e_v0 (double &obj, Vector3D &g_obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | g_fcn_3e_v1 (double &obj, Vector3D &g_obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | g_fcn_3e_v2 (double &obj, Vector3D &g_obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | h_fcn_3e_v3 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | h_fcn_3e_v0 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | h_fcn_3e_v1 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | h_fcn_3e_v2 (double &obj, Vector3D &g_obj, Matrix3D &h_obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c) |
| bool | m_fcn_3i (double &obj, const Vector3D x[4], const double a, const Exponent &b, const Exponent &c, const Vector3D &d) |
| bool | g_fcn_3i (double &obj, Vector3D g_obj[4], const Vector3D x[4], const double a, const Exponent &b, const Exponent &c, const Vector3D &d) |
| int | h_fcn_3i (double &obj, Vector3D g_obj[4], Matrix3D h_obj[10], const Vector3D x[4], const double a, const Exponent &b, const Exponent &c, const Vector3D &d) |
| void | test_aomd (void) |
| msq_stdio::ostream & | operator<< (msq_stdio::ostream &, const MsqError &) |
| Print message and stack trace. More... | |
| msq_stdio::ostream & | operator<< (msq_stdio::ostream &, const MsqError::Trace &) |
| Print MsqError::Trace. More... | |
| void | axpy (Vector3D res[], size_t size_r, const MsqHessian &H, const Vector3D x[], size_t size_x, const Vector3D y[], size_t size_y, MsqError &) |
| msq_stdio::ostream & | operator<< (msq_stdio::ostream &s, const MsqHessian &h) |
| Prints out the MsqHessian blocks. More... | |
| msq_stdio::ostream & | operator<< (msq_stdio::ostream &, StopWatchCollection &coll) |
| void | print_timing_diagnostics (int debugflag) |
| void | print_timing_diagnostics (msq_stdio::ostream &stream) |
| static msq_std::string | process_tstt_error (TSTTB::Error &tstt_err) |
| template<class T > | |
| static T * | convert_from_sidl_vector (sidl::array< T > &array) |
| template<class T > | |
| static sidl::array< T > | alloc_sidl_vector (size_t size) |
| template<class T > | |
| static sidl::array< T > | alloc_sidl_vector (size_t size, T init) |
| template<class S , class T > | |
| static void | copy_from_sidl (sidl::array< S > &source, T *target) |
| template<class T > | |
| static sidl::array< T > | convert_to_sidl_vector (T *array, size_t size) |
| const Vector3D | operator+ (const Vector3D &lhs, const Vector3D &rhs) |
| const Vector3D | operator- (const Vector3D &lhs, const Vector3D &rhs) |
| const Vector3D | operator* (const Vector3D &lhs, const double scalar) |
| const Vector3D | operator* (const double scalar, const Vector3D &rhs) |
| const Vector3D | operator/ (const Vector3D &lhs, const double scalar) |
| double | operator% (const Vector3D &lhs, const Vector3D &rhs) |
| double | inner (const Vector3D lhs[], const Vector3D rhs[], int n) |
| double | operator% (const double scalar, const Vector3D &rhs) |
| double | operator% (const Vector3D &lhs, const double scalar) |
| const Vector3D | operator* (const Vector3D &lhs, const Vector3D &rhs) |
| msq_stdio::ostream & | operator<< (msq_stdio::ostream &s, const Mesquite::Vector3D &v) |
| double | length (Vector3D *const v, int n) |
| double | Linf (Vector3D *const v, int n) |
| bool | operator== (const Vector3D &v1, const Vector3D &v2) |
| bool | operator!= (const Vector3D &v1, const Vector3D &v2) |
| ostream & | operator<< (ostream &stream, const MsqMeshEntity &entity) |
| ostream & | operator<< (ostream &stream, const PatchData &pd) |
| static msq_std::string | process_tstt_error (TSTTB::Error &tstt_err) |
| template<class T > | |
| static T * | convert_from_sidl_vector (sidl::array< T > &array) |
| template<class T > | |
| static sidl::array< T > | alloc_sidl_vector (size_t size) |
| template<class T > | |
| static sidl::array< T > | alloc_sidl_vector (size_t size, T init) |
| template<class S , class T > | |
| static void | copy_from_sidl (sidl::array< S > &source, T *target) |
| template<class T > | |
| static sidl::array< T > | convert_to_sidl_vector (T *array, size_t size) |
| void | msq_sigint_handler (int) |
Variables | |
| const int | MSQ_MAX_NUM_VERT_PER_ENT =8 |
| const int | MSQ_HIST_SIZE =7 |
| static const double | MSQ_SQRT_TWO = msq_stdc::sqrt(2.0) |
| static const double | MSQ_SQRT_THREE = msq_stdc::sqrt(3.0) |
| static const double | MSQ_SQRT_THREE_DIV_TWO =MSQ_SQRT_THREE/2.0 |
| static const double | MSQ_SQRT_THREE_INV =1.0/MSQ_SQRT_THREE |
| static const double | MSQ_SQRT_TWO_INV =1.0/MSQ_SQRT_TWO |
| static const double | MSQ_SQRT_TWO_DIV_SQRT_THREE =MSQ_SQRT_TWO/MSQ_SQRT_THREE |
| static const double | MSQ_ONE_THIRD = 1.0 / 3.0 |
| static const double | MSQ_TWO_THIRDS = 2.0 / 3.0 |
| static const double | MSQ_3RT_2_OVER_6RT_3 = msq_stdc::pow( 2/MSQ_SQRT_THREE, MSQ_ONE_THIRD ) |
| const unsigned | MSQ_UINT_MAX = ~(unsigned)0 |
| const int | MSQ_INT_MAX = MSQ_UINT_MAX >> 1 |
| const int | MSQ_INT_MIN = ~MSQ_INT_MAX |
| const double | MSQ_DBL_MIN = 1.0E-30 |
| const double | MSQ_MIN = MSQ_DBL_MIN |
| const double | MSQ_DBL_MAX = 1.0E30 |
| const double | MSQ_MAX = MSQ_DBL_MAX |
| const double | MSQ_MAX_CAP = 1.e6 |
| const char *const | VERTEX_BYTE_TAG_NAME = "MesquiteVertexByte" |
| The name of the tag (integer) that Mesquite will use to store internal data. More... | |
| const char *const | VERTEX_FIXED_TAG_NAME = "MesquiteVertexFixed" |
| The name of the tag (integer) Mesquite expects to be non-zero for vertices which are not to be moved by Mesquite. More... | |
| Mesquite::StopWatchCollection | GlobalStopWatches |
| const unsigned long | GRAD_FLAGS |
| const unsigned long | OF_FLAGS |
| const char *const | vtk_type_names [] |
| const msq_std::vector< size_t > | dummy_list |
| const Vector3D | dummy_vtx |
| msq_sig_handler_t | oldHandler = SIG_ERR |
| const int | DEFAULT_HISTOGRAM_INTERVALS = 10 |
Used to hold the error state and return it to the application.
Copyright 2003 Sandia Corporation and the University of Chicago. Under the terms of Contract DE-AC04-94AL85000 with Sandia Corporation and Contract W-31-109-ENG-38 with the University of Chicago, the U.S. Government retains certain rights in this software.
| typedef EntityIterator ElementIterator |
Definition at line 60 of file MeshInterface.hpp.
| typedef void(* msq_sig_handler_t)(int) |
Definition at line 34 of file Misc/MsqInterrupt.cpp.
| typedef double real |
Definition at line 84 of file Mesquite.hpp.
| typedef int StatusCode |
Definition at line 82 of file Mesquite.hpp.
| typedef void* TagHandle |
Type used to refer to a tag defintion.
Definition at line 63 of file MeshInterface.hpp.
| typedef EntityIterator VertexIterator |
Definition at line 58 of file MeshInterface.hpp.
| enum DomainHint |
A hint on the characteristics of the domain that Mesquite may use to determine what, if any, scheme to use to cache characteristics of the geometric domain.
| Enumerator | |
|---|---|
| NO_DOMAIN_HINT | |
| PLANAR_DOMAIN | |
| LOCAL_PALANAR | |
| SMOOTH_DOMAIN | |
Definition at line 446 of file MeshInterface.hpp.
| enum EntityTopology |
| Enumerator | |
|---|---|
| POLYGON | |
| TRIANGLE | |
| QUADRILATERAL | |
| POLYHEDRON | |
| TETRAHEDRON | |
| HEXAHEDRON | |
| PRISM | |
| PYRAMID | |
| SEPTAHEDRON | |
| MIXED | |
Definition at line 92 of file Mesquite.hpp.
| enum ReleaseType |
| Enumerator | |
|---|---|
| STABLE_RELEASE | |
| BETA | |
| ALPHA | |
Definition at line 111 of file Mesquite.hpp.
| enum StatusCodeValues |
| Enumerator | |
|---|---|
| MSQ_FAILURE | |
| MSQ_SUCCESS | |
Definition at line 86 of file Mesquite.hpp.
|
inlinestatic |
Definition at line 26 of file includeLinks/TSTTUtil.hpp.
Referenced by MeshTSTTImpl::tag_get_data(), and MeshTSTTImpl::tag_set_data().
|
inlinestatic |
Definition at line 26 of file src/Mesh/TSTTUtil.hpp.
|
inlinestatic |
Definition at line 33 of file includeLinks/TSTTUtil.hpp.
References convert_from_sidl_vector().

|
inlinestatic |
Definition at line 33 of file src/Mesh/TSTTUtil.hpp.
References convert_from_sidl_vector().

|
inline |
| res,: | array of Vector3D in which the result is stored. |
| size_r,: | size of the res array. |
| x,: | vector multiplied by the Hessian. |
| size_x,: | size of the x array. |
| y,: | vector added to the Hessian vector product. Set to 0 (NULL) if not needed. |
| size_y,: | size of the y array. Set to 0 if not needed. |
Definition at line 187 of file includeLinks/MsqHessian.hpp.
References eqAx(), i, j, MsqHessian::mColIndex, MsqHessian::mEntries, MsqHessian::mRowStart, MsqHessian::mSize, plusEqAx(), and plusEqTransAx().
| unsigned int build_number | ( | ) |
|
inline |
Definition at line 182 of file Mesquite.hpp.
References MSQ_ONE_THIRD, and pow().
Referenced by cbrt_sqr(), TargetCalculator::compute_Delta_3D(), TargetCalculator::compute_Lambda(), TargetCalculator::compute_Q_3D(), and Exponent::cubeRoot().

|
inline |
Definition at line 191 of file Mesquite.hpp.
References cbrt(), MSQ_TWO_THIRDS, and pow().
Referenced by Exponent::powTwoThirds().


|
inline |
Definition at line 76 of file includeLinks/LaplacianSmoother.hpp.
References PatchData::get_vertex_array(), MsqError::INVALID_ARG, j, and MSQ_SETERR.
Referenced by SmartLaplacianSmoother::optimize_vertex_positions(), and LaplacianSmoother::optimize_vertex_positions().

|
inlinestatic |
Definition at line 23 of file includeLinks/TSTTUtil.hpp.
Referenced by alloc_sidl_vector(), MeshTSTTImpl::cache_adjacent_elements(), GeomTSTTCommon::closest_and_normal(), GeomTSTTCommon::move_to(), GeomTSTTCommon::normal(), and MeshTSTTImpl::vertex_get_attached_elements().

|
inlinestatic |
Definition at line 23 of file src/Mesh/TSTTUtil.hpp.
|
inlinestatic |
Definition at line 51 of file includeLinks/TSTTUtil.hpp.
Referenced by GeomTSTTCommon::closest_and_normal(), MeshTSTTImpl::elements_get_attached_vertices(), MeshTSTTImpl::elements_get_topologies(), MeshTSTTImpl::get_all_mesh(), MeshTSTTImpl::get_vertex_use_count(), GeomTSTTCommon::move_to(), GeomTSTTCommon::normal(), MeshTSTTImpl::popupate_input_elements(), MeshTSTTImpl::tag_get_data(), MeshTSTTImpl::tag_set_data(), MeshTSTTImpl::vertex_set_coordinates(), MeshTSTTImpl::vertices_are_on_boundary(), MeshTSTTImpl::vertices_get_byte(), MeshTSTTImpl::vertices_get_coordinates(), and MeshTSTTImpl::vertices_set_byte().

|
inlinestatic |
Definition at line 51 of file src/Mesh/TSTTUtil.hpp.
|
inlinestatic |
Definition at line 42 of file includeLinks/TSTTUtil.hpp.
References i.
Referenced by MeshTSTTImpl::elements_get_attached_vertices().

|
inlinestatic |
|
inline |
Definition at line 549 of file includeLinks/Matrix3D.hpp.
References Matrix3D::v_.
Referenced by TargetCalculator::compute_Lambda(), TargetCalculator::compute_Q_3D(), TargetCalculator::compute_target_matrices_and_check_det(), sRI_DFT::evaluate_element(), sI_DFT::evaluate_element(), PatchData::get_barrier_delta(), Overlay_primitives::intersect(), intersect_triangle(), intersect_triangle1(), intersect_triangle2(), intersect_triangle3(), inv(), Aff_transformation_repS2< FT >::inverse(), FaceOffset_3::obtain_constrained_directions(), FaceOffset_3::solve_quadratic_func(), and timesInvA().
|
inline |
Definition at line 522 of file includeLinks/Matrix3D.hpp.
References Vector3D::mCoords, and Matrix3D::v_.
Referenced by axpy().

|
inline |
Return the square of the Frobenius norm of A, i.e. sum (diag (A' * A))
Definition at line 326 of file includeLinks/Matrix3D.hpp.
References i.
Referenced by sI_DFT::evaluate_element(), and sRI_DFT::evaluate_element().
|
inline |
Definition at line 170 of file includeLinks/MeanRatioFunctions.hpp.
References isqrt3, MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::compute_element_analytical_gradient(), and IdealWeightMeanRatio::compute_element_analytical_gradient().

|
inline |
Definition at line 584 of file includeLinks/MeanRatioFunctions.hpp.
References MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::compute_element_analytical_gradient(), and IdealWeightMeanRatio::compute_element_analytical_gradient().

|
inline |
Definition at line 973 of file includeLinks/MeanRatioFunctions.hpp.
References isqrt3, isqrt6, MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::compute_element_analytical_gradient(), and IdealWeightMeanRatio::compute_element_analytical_gradient().


|
inline |
Definition at line 1681 of file includeLinks/MeanRatioFunctions.hpp.
References g_fcn_3e_v3().

|
inline |
Definition at line 1693 of file includeLinks/MeanRatioFunctions.hpp.
References g_fcn_3e_v3().

|
inline |
Definition at line 1705 of file includeLinks/MeanRatioFunctions.hpp.
References g_fcn_3e_v3().

|
inline |
Definition at line 1629 of file includeLinks/MeanRatioFunctions.hpp.
References isqrt3, isqrt6, MSQ_MIN, pow(), and tisqrt6.
Referenced by g_fcn_3e_v0(), g_fcn_3e_v1(), and g_fcn_3e_v2().


|
inline |
Definition at line 1895 of file includeLinks/MeanRatioFunctions.hpp.
References MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::compute_element_analytical_gradient(), and IdealWeightMeanRatio::compute_element_analytical_gradient().

|
inline |
Definition at line 210 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient().


|
inline |
Definition at line 1216 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient().


|
inline |
Definition at line 1316 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient().


|
inline |
Definition at line 1408 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient().


|
inline |
Definition at line 709 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient().


|
inline |
Definition at line 2173 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient().


|
inline |
Definition at line 2279 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient().


|
inline |
Definition at line 2374 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient().


|
inline |
Definition at line 2466 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient().


|
inline |
Definition at line 244 of file includeLinks/MeanRatioFunctions.hpp.
References A, nvc::cross(), Matrix3D::fill_lower_triangle(), isqrt3, MSQ_MIN, pow(), and tisqrt3.
Referenced by IdealWeightInverseMeanRatio::compute_element_analytical_hessian(), and IdealWeightMeanRatio::compute_element_analytical_hessian().
|
inline |
Definition at line 656 of file includeLinks/MeanRatioFunctions.hpp.
References A, nvc::cross(), Matrix3D::fill_lower_triangle(), MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::compute_element_analytical_hessian(), and IdealWeightMeanRatio::compute_element_analytical_hessian().

|
inline |
Definition at line 1062 of file includeLinks/MeanRatioFunctions.hpp.
References A, nvc::cross(), Matrix3D::fill_lower_triangle(), isqrt3, isqrt6, MSQ_MIN, pow(), tisqrt3, and tisqrt6.
Referenced by IdealWeightInverseMeanRatio::compute_element_analytical_hessian(), and IdealWeightMeanRatio::compute_element_analytical_hessian().
|
inline |
Definition at line 1805 of file includeLinks/MeanRatioFunctions.hpp.
References h_fcn_3e_v3().

|
inline |
Definition at line 1818 of file includeLinks/MeanRatioFunctions.hpp.
References h_fcn_3e_v3().

|
inline |
Definition at line 1831 of file includeLinks/MeanRatioFunctions.hpp.
References h_fcn_3e_v3().

|
inline |
Definition at line 1717 of file includeLinks/MeanRatioFunctions.hpp.
References nvc::cross(), Matrix3D::fill_lower_triangle(), isqrt3, isqrt6, MSQ_MIN, pow(), and tisqrt6.
Referenced by h_fcn_3e_v0(), h_fcn_3e_v1(), and h_fcn_3e_v2().

|
inline |
Definition at line 1973 of file includeLinks/MeanRatioFunctions.hpp.
References A, nvc::cross(), Matrix3D::fill_lower_triangle(), MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::compute_element_analytical_hessian(), and IdealWeightMeanRatio::compute_element_analytical_hessian().
|
inline |
Definition at line 310 of file includeLinks/I_DFTFamilyFunctions.hpp.
References A, Matrix3D::fill_lower_triangle(), MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_hessian().

|
inline |
Definition at line 1497 of file includeLinks/I_DFTFamilyFunctions.hpp.
References A, Matrix3D::fill_lower_triangle(), MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_hessian().

|
inline |
Definition at line 1785 of file includeLinks/I_DFTFamilyFunctions.hpp.
References A, Matrix3D::fill_lower_triangle(), MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_hessian().


|
inline |
Definition at line 1999 of file includeLinks/I_DFTFamilyFunctions.hpp.
References A, Matrix3D::fill_lower_triangle(), MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_hessian().


|
inline |
Definition at line 815 of file includeLinks/I_DFTFamilyFunctions.hpp.
References A, Matrix3D::fill_lower_triangle(), MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_hessian().

|
inline |
Definition at line 2547 of file includeLinks/I_DFTFamilyFunctions.hpp.
References A, Matrix3D::fill_lower_triangle(), MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_hessian().

|
inline |
Definition at line 2865 of file includeLinks/I_DFTFamilyFunctions.hpp.
References A, Matrix3D::fill_lower_triangle(), MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_hessian().


|
inline |
Definition at line 3082 of file includeLinks/I_DFTFamilyFunctions.hpp.
References A, Matrix3D::fill_lower_triangle(), MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_hessian().

|
inline |
Definition at line 3259 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_hessian().


|
inline |
Dot product for arrays of Vector3Ds. see also operator% .
Definition at line 340 of file includeLinks/Vector3D.hpp.
Referenced by MsqHessian::cg_solver(), and FeasibleNewton::optimize_vertex_positions().

|
inline |
Definition at line 555 of file includeLinks/Matrix3D.hpp.
References det(), and Matrix3D::v_.
Referenced by circumcenterC3(), RI_DFT::compute_element_analytical_gradient(), I_DFT::compute_element_analytical_gradient(), RI_DFT::compute_element_analytical_hessian(), I_DFT::compute_element_analytical_hessian(), RI_DFT::evaluate_element(), and I_DFT::evaluate_element().

|
inline |
Definition at line 400 of file includeLinks/Vector3D.hpp.
Referenced by TerminationCriterion::accumulate_inner(), Rocblas::axpy_gen(), CImg< uintT >::blur_anisotropic(), Rocblas::calc(), Rocblas::calcDot(), MsqHessian::cg_solver(), COM_F_FUNC2(), GeneralizedConditionNumberQualityMetric::compute_condition_number(), MsqMeshEntity::compute_corner_normals(), MsqMeshEntity::compute_unsigned_area(), In_place_list_n< T, managed >::destroy(), CImg< uintT >::draw_arrow(), AspectRatioGammaQualityMetric::evaluate_element(), Rocblas::gen2arg(), init_structured_mesh(), init_unstructure_mesh(), initUnstructuredMesh(), io_hdf_data(), io_pane_connectivity(), main(), In_place_list_n< T, managed >::merge(), SphericalDomain::normal_at(), FeasibleNewton::optimize_vertex_positions(), tpz_ordered::parse_data(), tpz_fequad::parse_data(), Rocmop::perturb_stationary(), Randomize::randomize_vertex(), TerminationCriterion::reset_inner(), HDF4::SDgetdatastrs(), squared_sum(), MesqPane::tag_create(), and MeshTSTTImpl::tag_create().

|
inline |
Definition at line 409 of file includeLinks/Vector3D.hpp.
Referenced by ConjugateGradient::optimize_vertex_positions(), and TerminationCriterion::reset_inner().


|
inline |
Definition at line 131 of file includeLinks/MeanRatioFunctions.hpp.
References isqrt3, MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::evaluate_element(), and IdealWeightMeanRatio::evaluate_element().


|
inline |
Definition at line 543 of file includeLinks/MeanRatioFunctions.hpp.
References MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::evaluate_element(), and IdealWeightMeanRatio::evaluate_element().

|
inline |
Definition at line 931 of file includeLinks/MeanRatioFunctions.hpp.
References isqrt3, isqrt6, MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::evaluate_element(), and IdealWeightMeanRatio::evaluate_element().


|
inline |
Definition at line 1855 of file includeLinks/MeanRatioFunctions.hpp.
References MSQ_MIN, and pow().
Referenced by IdealWeightInverseMeanRatio::evaluate_element(), and IdealWeightMeanRatio::evaluate_element().

|
inline |
Definition at line 147 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient(), I_DFT::compute_element_analytical_hessian(), and I_DFT::evaluate_element().
|
inline |
Definition at line 643 of file includeLinks/I_DFTFamilyFunctions.hpp.
References MSQ_MIN, pow(), and sqrt().
Referenced by I_DFT::compute_element_analytical_gradient(), I_DFT::compute_element_analytical_hessian(), and I_DFT::evaluate_element().


| unsigned int major_version_number | ( | ) |
|
inline |
| unsigned int minor_version_number | ( | ) |
|
inline |
Definition at line 178 of file Mesquite.hpp.
|
inline |
Definition at line 177 of file Mesquite.hpp.
| void msq_sigint_handler | ( | int | ) |
Definition at line 38 of file Misc/MsqInterrupt.cpp.
References oldHandler, MsqInterrupt::set_handler(), and MsqInterrupt::set_interrupt().
Referenced by MsqInterrupt::set_handler().

|
inline |
Multiplies entry by entry. This is NOT a matrix multiplication.
Definition at line 312 of file includeLinks/Matrix3D.hpp.
References i.
|
inline |
|
inline |
Definition at line 442 of file includeLinks/Vector3D.hpp.
References Vector3D::mCoords.
|
inline |
|
inline |
|
inline |
Definition at line 357 of file includeLinks/Vector3D.hpp.
References Vector3D::mCoords.
|
inline |
Definition at line 309 of file includeLinks/Vector3D.hpp.
References Vector3D::x(), Vector3D::y(), and Vector3D::z().

|
inline |
Definition at line 316 of file includeLinks/Vector3D.hpp.
References Vector3D::x(), Vector3D::y(), and Vector3D::z().

|
inline |
|
inline |
|
inline |
friend function to allow for commutatative property of scalar mulitplication.
Definition at line 463 of file includeLinks/Matrix3D.hpp.
|
inline |
|
inline |
Computes 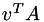 .
.
This function implicitly considers the transpose of vector x times the matrix A and it is implicit that the returned vector must be transposed.
Definition at line 510 of file includeLinks/Matrix3D.hpp.
|
inline |
|
inline |
Definition at line 295 of file includeLinks/Vector3D.hpp.
References Vector3D::x(), Vector3D::y(), and Vector3D::z().
|
inline |
|
inline |
Definition at line 302 of file includeLinks/Vector3D.hpp.
References Vector3D::x(), Vector3D::y(), and Vector3D::z().

|
inline |
Definition at line 323 of file includeLinks/Vector3D.hpp.
References Vector3D::x(), Vector3D::y(), and Vector3D::z().

| msq_stdio::ostream & operator<< | ( | msq_stdio::ostream & | str, |
| Mesquite::StopWatchCollection & | coll | ||
| ) |
Definition at line 311 of file Misc/MsqTimer.cpp.
References StopWatchCollection::get_keys_sorted_by_time(), StopWatchCollection::get_string(), i, StopWatchCollection::number_of_starts(), and StopWatchCollection::total_time().
|
inline |
Definition at line 250 of file includeLinks/Matrix3D.hpp.
| msq_stdio::ostream & operator<< | ( | msq_stdio::ostream & | s, |
| const MsqHessian & | h | ||
| ) |
Prints out the MsqHessian blocks.
Definition at line 507 of file Misc/MsqHessian.cpp.
References i, j, MsqHessian::mColIndex, MsqHessian::mEntries, MsqHessian::mRowStart, MsqHessian::mSize, and s.
| msq_stdio::ostream & operator<< | ( | msq_stdio::ostream & | s, |
| const Mesquite::Vector3D & | v | ||
| ) |
Definition at line 44 of file Misc/Vector3D.cpp.
| ostream & operator<< | ( | ostream & | stream, |
| const MsqMeshEntity & | entity | ||
| ) |
Definition at line 919 of file Mesh/MsqMeshEntity.cpp.
References i, MsqMeshEntity::vertex_count(), and MsqMeshEntity::vertexIndices.

| ostream & operator<< | ( | ostream & | stream, |
| const PatchData & | pd | ||
| ) |
Definition at line 1270 of file Mesh/PatchData.cpp.
References PatchData::AVERAGE_DET3D, PatchData::computedInfos, PatchData::domainSet, PatchData::elementArray, PatchData::ELEMENTS_ON_VERTEX_PATCH, PatchData::GLOBAL_PATCH, PatchData::have_computed_info(), PatchData::haveComputedInfos, HEXAHEDRON, i, if(), j, PatchData::MAX_EDGE_LENGTH, PatchData::MAX_UNSIGNED_AREA, PatchData::meshSet, PatchData::MIN_EDGE_LENGTH, PatchData::MIN_UNSIGNED_AREA, PatchData::MINMAX_SIGNED_DET2D, PatchData::MINMAX_SIGNED_DET3D, MsqVertex::MSQ_COORDS_CHANGED, MsqVertex::MSQ_HARD_FIXED, MsqVertex::MSQ_SOFT_FIXED, PatchData::mType, PatchData::num_elements(), PatchData::num_nodes(), PatchData::num_vertices(), POLYGON, POLYHEDRON, PRISM, PYRAMID, QUADRILATERAL, PatchDataMem< X >::size(), TETRAHEDRON, TRIANGLE, PatchData::vertAdjacencyArray, PatchData::vertAdjacencyOffsets, PatchData::vertexArray, and PatchData::VERTICES_ON_VERTEX_PATCH.

|
inline |
|
inline |
Definition at line 437 of file includeLinks/Vector3D.hpp.
References Vector3D::mCoords.
|
inline |
Definition at line 261 of file includeLinks/Matrix3D.hpp.
|
inline |
Definition at line 543 of file includeLinks/Matrix3D.hpp.
References Matrix3D::v_.
|
inline |
Definition at line 529 of file includeLinks/Matrix3D.hpp.
References Vector3D::mCoords, and Matrix3D::v_.
Referenced by axpy().

|
inline |
Definition at line 536 of file includeLinks/Matrix3D.hpp.
References Vector3D::mCoords, and Matrix3D::v_.
Referenced by axpy().

|
inline |
Definition at line 89 of file includeLinks/Exponent.hpp.
References Exponent::raise().
Referenced by CImg< uintT >::_draw_ellipse(), QualityMetric::average_metrics(), QualityAssessor::Assessor::calculate_histogram_range(), cbrt(), cbrt_sqr(), IdealWeightInverseMeanRatio::compute_element_analytical_hessian(), Alg_Metric_Base_3::compute_shape(), Alg_Metric_Base_3::compute_skew(), dist(), MVec::distance_between(), CImg< uintT >::draw_axis(), CImg< uintT >::edge_tensors(), CImg< T >::_cimg_math_parser::eval(), sRI_DFT::evaluate_element(), sI_DFT::evaluate_element(), PowerQualityMetric::evaluate_element(), PowerQualityMetric::evaluate_vertex(), g_fcn_2e(), g_fcn_2i(), g_fcn_3e(), g_fcn_3e_v3(), g_fcn_3i(), g_fcn_ridft2(), g_fcn_ridft3(), g_gdft_2(), g_gdft_2_v0(), g_gdft_2_v1(), g_gdft_2_v2(), g_gdft_3(), g_gdft_3_v0(), g_gdft_3_v1(), g_gdft_3_v2(), g_gdft_3_v3(), CImg< uintT >::get_displacement_field(), CImg< uintT >::get_select_graph(), h_fcn_2e(), h_fcn_2i(), h_fcn_3e(), h_fcn_3e_v3(), h_fcn_3i(), h_fcn_ridft2(), h_fcn_ridft3(), h_gdft_2(), h_gdft_2_v0(), h_gdft_2_v1(), h_gdft_2_v2(), h_gdft_3(), h_gdft_3_v0(), h_gdft_3_v1(), h_gdft_3_v2(), h_gdft_3_v3(), TargetCalculator::initialize_default_target_matrices(), CImg< uintT >::LabtoXYZ(), m_fcn_2e(), m_fcn_2i(), m_fcn_3e(), m_fcn_3i(), m_fcn_ridft2(), m_fcn_ridft3(), m_gdft_2(), m_gdft_3(), CImg< uintT >::pow(), CImg< uintT >::RGBtoHSI(), IdealWeightInverseMeanRatio::set_metric_power(), CImg< uintT >::sharpen(), Exponent::std_pow(), and TRAIL_TimeString().

|
inline |
Definition at line 188 of file includeLinks/MsqTimer.hpp.
References GlobalStopWatches, and MSQ_DBGOUT.
|
inline |
Definition at line 191 of file includeLinks/MsqTimer.hpp.
References GlobalStopWatches.
|
inlinestatic |
Definition at line 9 of file src/Mesh/TSTTUtil.hpp.
References MSQ_DBGOUT.
|
inlinestatic |
Definition at line 9 of file includeLinks/TSTTUtil.hpp.
References MSQ_DBGOUT.
Referenced by MeshTSTTImpl::cache_adjacent_elements(), DomainTSTT::closest_point(), GeomEntTSTT::closest_point(), GeomTSTT::create(), MeshTSTTImpl::element_get_attached_vertex_count(), MeshTSTTImpl::element_get_topology(), MeshTSTTImpl::element_iterator(), MeshTSTTImpl::elements_get_attached_vertices(), MeshTSTTImpl::elements_get_topologies(), MeshTSTTImpl::get_all_mesh(), MeshTSTTImpl::get_all_sizes(), MeshTSTTImpl::get_geometric_dimension(), MeshTSTTImpl::get_vertex_use_count(), MeshTSTTImpl::MeshTSTTImpl(), DomainTSTT::normal_at(), GeomEntTSTT::normal_at(), TSTTIterator::operator++(), TSTTArrIter::operator++(), TSTTIterator::restart(), TSTTArrIter::restart(), MeshTSTTImpl::set_active_set(), MeshTSTTImpl::set_int_tag(), DomainTSTT::snap_to(), GeomEntTSTT::snap_to(), MeshTSTTImpl::tag_create(), MeshTSTTImpl::tag_delete(), MeshTSTTImpl::tag_get(), MeshTSTTImpl::tag_get_data(), MeshTSTTImpl::tag_properties(), MeshTSTTImpl::tag_set_data(), TSTTIterator::TSTTIterator(), MeshTSTTImpl::vertex_get_byte(), MeshTSTTImpl::vertex_is_fixed(), MeshTSTTImpl::vertex_iterator(), MeshTSTTImpl::vertex_set_byte(), MeshTSTTImpl::vertex_set_coordinates(), MeshTSTTImpl::vertices_are_on_boundary(), MeshTSTTImpl::vertices_get_byte(), MeshTSTTImpl::vertices_get_coordinates(), MeshTSTTImpl::vertices_set_byte(), MeshTSTTImpl::~MeshTSTTImpl(), and TSTTArrIter::~TSTTArrIter().

|
inline |
Definition at line 593 of file includeLinks/Matrix3D.hpp.
Referenced by I_DFT::compute_element_analytical_gradient(), I_DFT::compute_element_analytical_hessian(), and I_DFT::evaluate_element().

| Mesquite::ReleaseType release_type | ( | ) |
Definition at line 61 of file Misc/MesquiteVersion.cpp.
References ALPHA.
| void test_aomd | ( | void | ) |
|
inline |
Definition at line 572 of file includeLinks/Matrix3D.hpp.
References det(), and Matrix3D::v_.
Referenced by DistanceFromTarget::compute_T_matrices().

|
inline |
Definition at line 335 of file includeLinks/Matrix3D.hpp.
References i.
Referenced by RI_DFT::compute_element_analytical_hessian(), IdealWeightInverseMeanRatio::compute_element_analytical_hessian(), IdealWeightMeanRatio::compute_element_analytical_hessian(), I_DFT::compute_element_analytical_hessian(), and sRI_DFT::evaluate_element().

| const char * version_string | ( | bool | include_build_number = false | ) |
Definition at line 39 of file Misc/MesquiteVersion.cpp.
References MSQ_BUILD_STRING, and MSQ_VERSION_STRING.
Referenced by InstructionQueue::run_instructions().

|
inline |
Definition at line 530 of file MeshInterface.hpp.
| const int DEFAULT_HISTOGRAM_INTERVALS = 10 |
Definition at line 62 of file QualityAssessor/QualityAssessor.cpp.
Referenced by QualityAssessor::add_quality_assessment().
| const msq_std::vector< size_t > dummy_list |
Definition at line 37 of file Mesh/MeshImplData.cpp.
Referenced by MeshImplData::element_connectivity(), and MeshImplData::vertex_adjacencies().
| const Vector3D dummy_vtx |
Definition at line 38 of file Mesh/MeshImplData.cpp.
Referenced by MeshImplData::get_vertex_coords().
| Mesquite::StopWatchCollection GlobalStopWatches |
Definition at line 186 of file src/Misc/MsqTimer.hpp.
Referenced by print_timing_diagnostics(), FunctionTimer::start(), and FunctionTimer::~FunctionTimer().
| const unsigned long GRAD_FLAGS |
Definition at line 51 of file Control/TerminationCriterion.cpp.
Referenced by TerminationCriterion::accumulate_inner(), TerminationCriterion::accumulate_outer(), TerminationCriterion::reset_inner(), and TerminationCriterion::reset_outer().
|
static |
Definition at line 130 of file Mesquite.hpp.
Referenced by MsqMeshEntity::compute_corner_matrices(), RI_DFT::compute_element_analytical_gradient(), I_DFT::compute_element_analytical_gradient(), RI_DFT::compute_element_analytical_hessian(), I_DFT::compute_element_analytical_hessian(), RI_DFT::evaluate_element(), I_DFT::evaluate_element(), and TargetCalculator::initialize_default_target_matrices().
| const double MSQ_DBL_MAX = 1.0E30 |
Definition at line 170 of file Mesquite.hpp.
Referenced by PatchData::get_barrier_delta(), and PatchData::get_minmax_element_unsigned_area().
| const double MSQ_DBL_MIN = 1.0E-30 |
Definition at line 158 of file Mesquite.hpp.
Referenced by ShapeQualityMetric::condition_number_2d(), ShapeQualityMetric::condition_number_3d(), and DistanceFromTarget::get_barrier_function().
| const int MSQ_HIST_SIZE =7 |
Definition at line 121 of file Mesquite.hpp.
| const int MSQ_INT_MAX = MSQ_UINT_MAX >> 1 |
Definition at line 141 of file Mesquite.hpp.
| const int MSQ_INT_MIN = ~MSQ_INT_MAX |
Definition at line 147 of file Mesquite.hpp.
| const double MSQ_MAX = MSQ_DBL_MAX |
Definition at line 172 of file Mesquite.hpp.
Referenced by NonSmoothSteepestDescent::find_active_set().
| const double MSQ_MAX_CAP = 1.e6 |
Definition at line 173 of file Mesquite.hpp.
Referenced by QualityMetric::average_metrics(), GeneralizedConditionNumberQualityMetric::compute_condition_number(), ShapeQualityMetric::condition_number_2d(), ShapeQualityMetric::condition_number_3d(), ConditionNumberQualityMetric::evaluate_element(), CornerJacobianQualityMetric::evaluate_element(), UntangleBetaQualityMetric::evaluate_element(), AspectRatioGammaQualityMetric::evaluate_element(), VertexConditionNumberQualityMetric::evaluate_vertex(), and ConjugateGradient::optimize_vertex_positions().
| const int MSQ_MAX_NUM_VERT_PER_ENT =8 |
Definition at line 120 of file Mesquite.hpp.
Referenced by LPtoPTemplate::compute_analytical_gradient(), LPtoPTemplate::compute_analytical_hessian(), TargetCalculator::compute_reference_corner_matrices(), WTargetCalculator::compute_target_matrices(), LVQDTargetCalculator::compute_target_matrices(), sRI_DFT::evaluate_element(), ConditionNumberQualityMetric::evaluate_element(), sI_DFT::evaluate_element(), UntangleBetaQualityMetric::evaluate_element(), PatchData::get_average_Lambda_3d(), and PatchData::get_barrier_delta().
| const double MSQ_MIN = MSQ_DBL_MIN |
Definition at line 160 of file Mesquite.hpp.
Referenced by QualityMetric::average_metric_and_weights(), QualityMetric::average_metrics(), GeneralizedConditionNumberQualityMetric::compute_condition_number(), ASMQualityMetric::evaluate_element(), AspectRatioGammaQualityMetric::evaluate_element(), g_fcn_2e(), g_fcn_2i(), g_fcn_3e(), g_fcn_3e_v3(), g_fcn_3i(), g_fcn_ridft2(), g_fcn_ridft3(), g_gdft_2(), g_gdft_2_v0(), g_gdft_2_v1(), g_gdft_2_v2(), g_gdft_3(), g_gdft_3_v0(), g_gdft_3_v1(), g_gdft_3_v2(), g_gdft_3_v3(), PatchData::get_barrier_delta(), ConjugateGradient::get_step(), h_fcn_2e(), h_fcn_2i(), h_fcn_3e(), h_fcn_3e_v3(), h_fcn_3i(), h_fcn_ridft2(), h_fcn_ridft3(), h_gdft_2(), h_gdft_2_v0(), h_gdft_2_v1(), h_gdft_2_v2(), h_gdft_3(), h_gdft_3_v0(), h_gdft_3_v1(), h_gdft_3_v2(), h_gdft_3_v3(), m_fcn_2e(), m_fcn_2i(), m_fcn_3e(), m_fcn_3i(), m_fcn_ridft2(), m_fcn_ridft3(), m_gdft_2(), m_gdft_3(), PowerQualityMetric::PowerQualityMetric(), and IdealWeightInverseMeanRatio::set_metric_power().
|
static |
Definition at line 128 of file Mesquite.hpp.
Referenced by cbrt(), RI_DFT::compute_element_analytical_gradient(), I_DFT::compute_element_analytical_gradient(), RI_DFT::compute_element_analytical_hessian(), I_DFT::compute_element_analytical_hessian(), sI_DFT::evaluate_element(), sRI_DFT::evaluate_element(), RI_DFT::evaluate_element(), and I_DFT::evaluate_element().
|
static |
Definition at line 123 of file Mesquite.hpp.
Referenced by ConditionNumberQualityMetric::evaluate_element(), UntangleBetaQualityMetric::evaluate_element(), VertexConditionNumberQualityMetric::evaluate_vertex(), and TargetCalculator::initialize_default_target_matrices().
|
static |
Definition at line 124 of file Mesquite.hpp.
|
static |
Definition at line 125 of file Mesquite.hpp.
Referenced by MsqMeshEntity::compute_weighted_jacobian(), ConditionNumberQualityMetric::evaluate_element(), UntangleBetaQualityMetric::evaluate_element(), and VertexConditionNumberQualityMetric::evaluate_vertex().
|
static |
Definition at line 122 of file Mesquite.hpp.
Referenced by ConditionNumberQualityMetric::evaluate_element(), UntangleBetaQualityMetric::evaluate_element(), VertexConditionNumberQualityMetric::evaluate_vertex(), and TargetCalculator::initialize_default_target_matrices().
|
static |
Definition at line 127 of file Mesquite.hpp.
|
static |
Definition at line 126 of file Mesquite.hpp.
Referenced by MsqMeshEntity::compute_weighted_jacobian().
|
static |
Definition at line 129 of file Mesquite.hpp.
Referenced by cbrt_sqr(), sI_DFT::evaluate_element(), and I_DFT::I_DFT().
| const unsigned MSQ_UINT_MAX = ~(unsigned)0 |
Definition at line 135 of file Mesquite.hpp.
| const unsigned long OF_FLAGS |
Definition at line 55 of file Control/TerminationCriterion.cpp.
Referenced by TerminationCriterion::accumulate_inner(), TerminationCriterion::accumulate_outer(), TerminationCriterion::reset_inner(), and TerminationCriterion::reset_outer().
| msq_sig_handler_t oldHandler = SIG_ERR |
Definition at line 35 of file Misc/MsqInterrupt.cpp.
Referenced by MsqInterrupt::allow(), MsqInterrupt::disable(), MsqInterrupt::enable(), msq_sigint_handler(), MsqInterrupt::set_handler(), and MsqInterrupt::~MsqInterrupt().
| const char *const VERTEX_BYTE_TAG_NAME = "MesquiteVertexByte" |
The name of the tag (integer) that Mesquite will use to store internal data.
Definition at line 64 of file includeLinks/MeshTSTT.hpp.
Referenced by MeshTSTTImpl::MeshTSTTImpl().
| const char *const VERTEX_FIXED_TAG_NAME = "MesquiteVertexFixed" |
The name of the tag (integer) Mesquite expects to be non-zero for vertices which are not to be moved by Mesquite.
Definition at line 69 of file includeLinks/MeshTSTT.hpp.
Referenced by MeshTSTTImpl::MeshTSTTImpl().
| const char *const vtk_type_names |
Definition at line 1156 of file Mesh/MeshImpl.cpp.
Referenced by MeshImpl::vtk_read_field(), MeshImpl::vtk_read_polydata(), MeshImpl::vtk_read_rectilinear_grid(), MeshImpl::vtk_read_scalar_attrib(), MeshImpl::vtk_read_structured_grid(), MeshImpl::vtk_read_tensor_attrib(), MeshImpl::vtk_read_texture_attrib(), MeshImpl::vtk_read_unstructured_grid(), and MeshImpl::vtk_read_vector_attrib().