Class containing the target corner matrices for the context based smoothing. More...
#include <RI_DFT.hpp>
Public Member Functions | |
| RI_DFT () | |
| virtual | ~RI_DFT () |
| virtual destructor ensures use of polymorphism during destruction More... | |
| bool | evaluate_element (PatchData &pd, MsqMeshEntity *e, double &m, MsqError &err) |
| Evaluate the metric for an element. More... | |
| bool | compute_element_analytical_gradient (PatchData &pd, MsqMeshEntity *e, MsqVertex *fv[], Vector3D g[], int nfv, double &m, MsqError &err) |
| Virtual function that computes the gradient of the QualityMetric analytically. The base class implementation of this function simply prints a warning and calls compute_numerical_gradient to calculate the gradient. This is used by metric which mType is ELEMENT_BASED. For parameters, see compute_element_gradient() . More... | |
| bool | compute_element_analytical_hessian (PatchData &pd, MsqMeshEntity *e, MsqVertex *fv[], Vector3D g[], Matrix3D h[], int nfv, double &m, MsqError &err) |
| RI_DFT () | |
| virtual | ~RI_DFT () |
| virtual destructor ensures use of polymorphism during destruction More... | |
| bool | evaluate_element (PatchData &pd, MsqMeshEntity *e, double &m, MsqError &err) |
| Evaluate the metric for an element. More... | |
| bool | compute_element_analytical_gradient (PatchData &pd, MsqMeshEntity *e, MsqVertex *fv[], Vector3D g[], int nfv, double &m, MsqError &err) |
| Virtual function that computes the gradient of the QualityMetric analytically. The base class implementation of this function simply prints a warning and calls compute_numerical_gradient to calculate the gradient. This is used by metric which mType is ELEMENT_BASED. For parameters, see compute_element_gradient() . More... | |
| bool | compute_element_analytical_hessian (PatchData &pd, MsqMeshEntity *e, MsqVertex *fv[], Vector3D g[], Matrix3D h[], int nfv, double &m, MsqError &err) |
 Public Member Functions inherited from DistanceFromTarget Public Member Functions inherited from DistanceFromTarget | |
| virtual | ~DistanceFromTarget () |
| virtual destructor ensures use of polymorphism during destruction More... | |
| virtual | ~DistanceFromTarget () |
| virtual destructor ensures use of polymorphism during destruction More... | |
 Public Member Functions inherited from QualityMetric Public Member Functions inherited from QualityMetric | |
| virtual | ~QualityMetric () |
| MetricType | get_metric_type () |
| void | set_element_evaluation_mode (ElementEvaluationMode mode, MsqError &err) |
| Sets the evaluation mode for the ELEMENT_BASED metrics. More... | |
| ElementEvaluationMode | get_element_evaluation_mode () |
| Returns the evaluation mode for the metric. More... | |
| void | set_averaging_method (AveragingMethod method, MsqError &err) |
| void | set_feasible_constraint (int alpha) |
| int | get_feasible_constraint () |
| Returns the feasible flag for this metric. More... | |
| void | set_name (msq_std::string st) |
| Sets the name of this metric. More... | |
| msq_std::string | get_name () |
| Returns the name of this metric (as a string). More... | |
| double | vertex_barrier_function (double det, double delta) |
| Escobar Barrier Function for Shape and Other Metrics. More... | |
| virtual bool | evaluate_vertex (PatchData &, MsqVertex *, double &, MsqError &err) |
| Evaluate the metric for a vertex. More... | |
| void | set_gradient_type (GRADIENT_TYPE grad) |
| Sets gradType for this metric. More... | |
| void | set_hessian_type (HESSIAN_TYPE ht) |
| Sets hessianType for this metric. More... | |
| bool | compute_vertex_gradient (PatchData &pd, MsqVertex &vertex, MsqVertex *vertices[], Vector3D grad_vec[], int num_vtx, double &metric_value, MsqError &err) |
| Calls compute_vertex_numerical_gradient if gradType equals NUMERCIAL_GRADIENT. Calls compute_vertex_analytical_gradient if gradType equals ANALYTICAL_GRADIENT;. More... | |
| bool | compute_element_gradient (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], int num_free_vtx, double &metric_value, MsqError &err) |
| For MetricType == ELEMENT_BASED. Calls either compute_element_numerical_gradient() or compute_element_analytical_gradient() for gradType equal NUMERICAL_GRADIENT or ANALYTICAL_GRADIENT, respectively. More... | |
| bool | compute_element_gradient_expanded (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], int num_free_vtx, double &metric_value, MsqError &err) |
| bool | compute_element_hessian (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], Matrix3D hessian[], int num_free_vtx, double &metric_value, MsqError &err) |
| For MetricType == ELEMENT_BASED. Calls either compute_element_numerical_hessian() or compute_element_analytical_hessian() for hessianType equal NUMERICAL_HESSIAN or ANALYTICAL_HESSIAN, respectively. More... | |
| void | set_negate_flag (int neg) |
| int | get_negate_flag () |
| Returns negateFlag. More... | |
| virtual void | change_metric_type (MetricType t, MsqError &err) |
| virtual | ~QualityMetric () |
| MetricType | get_metric_type () |
| void | set_element_evaluation_mode (ElementEvaluationMode mode, MsqError &err) |
| Sets the evaluation mode for the ELEMENT_BASED metrics. More... | |
| ElementEvaluationMode | get_element_evaluation_mode () |
| Returns the evaluation mode for the metric. More... | |
| void | set_averaging_method (AveragingMethod method, MsqError &err) |
| void | set_feasible_constraint (int alpha) |
| int | get_feasible_constraint () |
| Returns the feasible flag for this metric. More... | |
| void | set_name (msq_std::string st) |
| Sets the name of this metric. More... | |
| msq_std::string | get_name () |
| Returns the name of this metric (as a string). More... | |
| double | vertex_barrier_function (double det, double delta) |
| Escobar Barrier Function for Shape and Other Metrics. More... | |
| virtual bool | evaluate_vertex (PatchData &, MsqVertex *, double &, MsqError &err) |
| Evaluate the metric for a vertex. More... | |
| void | set_gradient_type (GRADIENT_TYPE grad) |
| Sets gradType for this metric. More... | |
| void | set_hessian_type (HESSIAN_TYPE ht) |
| Sets hessianType for this metric. More... | |
| bool | compute_vertex_gradient (PatchData &pd, MsqVertex &vertex, MsqVertex *vertices[], Vector3D grad_vec[], int num_vtx, double &metric_value, MsqError &err) |
| bool | compute_element_gradient (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], int num_free_vtx, double &metric_value, MsqError &err) |
| For MetricType == ELEMENT_BASED. Calls either compute_element_numerical_gradient() or compute_element_analytical_gradient() for gradType equal NUMERICAL_GRADIENT or ANALYTICAL_GRADIENT, respectively. More... | |
| bool | compute_element_gradient_expanded (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], int num_free_vtx, double &metric_value, MsqError &err) |
| bool | compute_element_hessian (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], Matrix3D hessian[], int num_free_vtx, double &metric_value, MsqError &err) |
| For MetricType == ELEMENT_BASED. Calls either compute_element_numerical_hessian() or compute_element_analytical_hessian() for hessianType equal NUMERICAL_HESSIAN or ANALYTICAL_HESSIAN, respectively. More... | |
| void | set_negate_flag (int neg) |
| int | get_negate_flag () |
| Returns negateFlag. More... | |
| virtual void | change_metric_type (MetricType t, MsqError &err) |
Private Attributes | |
| double | a |
| Exponent | b |
| Exponent | c |
| Vector3D | mNormal |
| Vector3D | mCoords [4] |
| Vector3D | mGrads [4] |
| Vector3D | mAccGrads [8] |
| Matrix3D | mHessians [10] |
| Matrix3D | invW |
Additional Inherited Members | |
 Public Types inherited from QualityMetric Public Types inherited from QualityMetric | |
| enum | MetricType { MT_UNDEFINED, VERTEX_BASED, ELEMENT_BASED, VERTEX_BASED_FREE_ONLY, MT_UNDEFINED, VERTEX_BASED, ELEMENT_BASED, VERTEX_BASED_FREE_ONLY } |
| enum | ElementEvaluationMode { EEM_UNDEFINED, ELEMENT_VERTICES, LINEAR_GAUSS_POINTS, QUADRATIC_GAUSS_POINTS, CUBIC_GAUSS_POINTS, EEM_UNDEFINED, ELEMENT_VERTICES, LINEAR_GAUSS_POINTS, QUADRATIC_GAUSS_POINTS, CUBIC_GAUSS_POINTS } |
| enum | AveragingMethod { NONE, LINEAR, RMS, HMS, MINIMUM, MAXIMUM, HARMONIC, GEOMETRIC, SUM, SUM_SQUARED, GENERALIZED_MEAN, STANDARD_DEVIATION, MAX_OVER_MIN, MAX_MINUS_MIN, SUM_OF_RATIOS_SQUARED, NONE, LINEAR, RMS, HMS, MINIMUM, MAXIMUM, HARMONIC, GEOMETRIC, SUM, SUM_SQUARED, GENERALIZED_MEAN, STANDARD_DEVIATION, MAX_OVER_MIN, MAX_MINUS_MIN, SUM_OF_RATIOS_SQUARED } |
| enum | GRADIENT_TYPE { NUMERICAL_GRADIENT, ANALYTICAL_GRADIENT, NUMERICAL_GRADIENT, ANALYTICAL_GRADIENT } |
| enum | HESSIAN_TYPE { NUMERICAL_HESSIAN, ANALYTICAL_HESSIAN, NUMERICAL_HESSIAN, ANALYTICAL_HESSIAN } |
| enum | MetricType { MT_UNDEFINED, VERTEX_BASED, ELEMENT_BASED, VERTEX_BASED_FREE_ONLY, MT_UNDEFINED, VERTEX_BASED, ELEMENT_BASED, VERTEX_BASED_FREE_ONLY } |
| enum | ElementEvaluationMode { EEM_UNDEFINED, ELEMENT_VERTICES, LINEAR_GAUSS_POINTS, QUADRATIC_GAUSS_POINTS, CUBIC_GAUSS_POINTS, EEM_UNDEFINED, ELEMENT_VERTICES, LINEAR_GAUSS_POINTS, QUADRATIC_GAUSS_POINTS, CUBIC_GAUSS_POINTS } |
| enum | AveragingMethod { NONE, LINEAR, RMS, HMS, MINIMUM, MAXIMUM, HARMONIC, GEOMETRIC, SUM, SUM_SQUARED, GENERALIZED_MEAN, STANDARD_DEVIATION, MAX_OVER_MIN, MAX_MINUS_MIN, SUM_OF_RATIOS_SQUARED, NONE, LINEAR, RMS, HMS, MINIMUM, MAXIMUM, HARMONIC, GEOMETRIC, SUM, SUM_SQUARED, GENERALIZED_MEAN, STANDARD_DEVIATION, MAX_OVER_MIN, MAX_MINUS_MIN, SUM_OF_RATIOS_SQUARED } |
| enum | GRADIENT_TYPE { NUMERICAL_GRADIENT, ANALYTICAL_GRADIENT, NUMERICAL_GRADIENT, ANALYTICAL_GRADIENT } |
| enum | HESSIAN_TYPE { NUMERICAL_HESSIAN, ANALYTICAL_HESSIAN, NUMERICAL_HESSIAN, ANALYTICAL_HESSIAN } |
 Protected Member Functions inherited from DistanceFromTarget Protected Member Functions inherited from DistanceFromTarget | |
| void | compute_T_matrices (MsqMeshEntity &elem, PatchData &pd, Matrix3D T[], size_t num_T, double c_k[], MsqError &err) |
For a given element, compute each corner matrix A, and given a target corner matrix W, returns 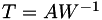 for each corner. More... for each corner. More... | |
| bool | get_barrier_function (PatchData &pd, const double &tau, double &h, MsqError &err) |
| void | compute_T_matrices (MsqMeshEntity &elem, PatchData &pd, Matrix3D T[], size_t num_T, double c_k[], MsqError &err) |
For a given element, compute each corner matrix A, and given a target corner matrix W, returns 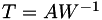 for each corner. More... for each corner. More... | |
| bool | get_barrier_function (PatchData &pd, const double &tau, double &h, MsqError &err) |
 Protected Member Functions inherited from QualityMetric Protected Member Functions inherited from QualityMetric | |
| QualityMetric () | |
| void | set_metric_type (MetricType t) |
| This function should be used in the constructor of every concrete quality metric. More... | |
| double | average_metrics (const double metric_values[], const int &num_values, MsqError &err) |
| average_metrics takes an array of length num_values and averages the contents using averaging method data member avgMethod . More... | |
| double | average_metric_and_weights (double metric_values[], int num_metric_values, MsqError &err) |
| Given a list of metric values, calculate the average metric valude according to the current avgMethod and write into the passed metric_values array the the value weight/count to use when averaging gradient vectors for the metric. More... | |
| double | weighted_average_metrics (const double coef[], const double metric_values[], const int &num_values, MsqError &err) |
| takes an array of coefficients and an array of metrics (both of length num_value) and averages the contents using averaging method 'method'. More... | |
| bool | compute_vertex_numerical_gradient (PatchData &pd, MsqVertex &vertex, MsqVertex *vertices[], Vector3D grad_vec[], int num_vtx, double &metric_value, MsqError &err) |
| bool | compute_element_numerical_gradient (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], int num_free_vtx, double &metric_value, MsqError &err) |
| Non-virtual function which numerically computes the gradient of a QualityMetric of a given element for a given set of free vertices on that element. This is used by metric which mType is ELEMENT_BASED. For parameters, see compute_element_gradient() . More... | |
| virtual bool | compute_vertex_analytical_gradient (PatchData &pd, MsqVertex &vertex, MsqVertex *vertices[], Vector3D grad_vec[], int num_vtx, double &metric_value, MsqError &err) |
| Virtual function that computes the gradient of the QualityMetric analytically. The base class implementation of this function simply prints a warning and calls compute_numerical_gradient to calculate the gradient. This is used by metric which mType is VERTEX_BASED. More... | |
| bool | compute_element_numerical_hessian (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], Matrix3D hessian[], int num_free_vtx, double &metric_value, MsqError &err) |
| QualityMetric () | |
| void | set_metric_type (MetricType t) |
| This function should be used in the constructor of every concrete quality metric. More... | |
| double | average_metrics (const double metric_values[], const int &num_values, MsqError &err) |
| average_metrics takes an array of length num_values and averages the contents using averaging method data member avgMethod . More... | |
| double | average_metric_and_weights (double metric_values[], int num_metric_values, MsqError &err) |
| Given a list of metric values, calculate the average metric valude according to the current avgMethod and write into the passed metric_values array the the value weight/count to use when averaging gradient vectors for the metric. More... | |
| double | weighted_average_metrics (const double coef[], const double metric_values[], const int &num_values, MsqError &err) |
| takes an array of coefficients and an array of metrics (both of length num_value) and averages the contents using averaging method 'method'. More... | |
| bool | compute_vertex_numerical_gradient (PatchData &pd, MsqVertex &vertex, MsqVertex *vertices[], Vector3D grad_vec[], int num_vtx, double &metric_value, MsqError &err) |
| bool | compute_element_numerical_gradient (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], int num_free_vtx, double &metric_value, MsqError &err) |
| Non-virtual function which numerically computes the gradient of a QualityMetric of a given element for a given set of free vertices on that element. This is used by metric which mType is ELEMENT_BASED. For parameters, see compute_element_gradient() . More... | |
| virtual bool | compute_vertex_analytical_gradient (PatchData &pd, MsqVertex &vertex, MsqVertex *vertices[], Vector3D grad_vec[], int num_vtx, double &metric_value, MsqError &err) |
| Virtual function that computes the gradient of the QualityMetric analytically. The base class implementation of this function simply prints a warning and calls compute_numerical_gradient to calculate the gradient. This is used by metric which mType is VERTEX_BASED. More... | |
| bool | compute_element_numerical_hessian (PatchData &pd, MsqMeshEntity *element, MsqVertex *free_vtces[], Vector3D grad_vec[], Matrix3D hessian[], int num_free_vtx, double &metric_value, MsqError &err) |
 Protected Attributes inherited from QualityMetric Protected Attributes inherited from QualityMetric | |
| AveragingMethod | avgMethod |
| int | feasible |
| msq_std::string | metricName |
Class containing the target corner matrices for the context based smoothing.
Definition at line 51 of file includeLinks/RI_DFT.hpp.
|
inline |
Definition at line 55 of file includeLinks/RI_DFT.hpp.
References QualityMetric::ELEMENT_BASED, QualityMetric::LINEAR, MSQ_CHKERR, QualityMetric::NUMERICAL_GRADIENT, QualityMetric::NUMERICAL_HESSIAN, QualityMetric::set_averaging_method(), QualityMetric::set_gradient_type(), QualityMetric::set_hessian_type(), and QualityMetric::set_metric_type().
|
inlinevirtual |
virtual destructor ensures use of polymorphism during destruction
Definition at line 66 of file includeLinks/RI_DFT.hpp.
|
inline |
Definition at line 55 of file src/QualityMetric/DFT/RI_DFT.hpp.
References QualityMetric::ELEMENT_BASED, QualityMetric::LINEAR, MSQ_CHKERR, QualityMetric::NUMERICAL_GRADIENT, QualityMetric::NUMERICAL_HESSIAN, QualityMetric::set_averaging_method(), QualityMetric::set_gradient_type(), QualityMetric::set_hessian_type(), and QualityMetric::set_metric_type().

|
inlinevirtual |
virtual destructor ensures use of polymorphism during destruction
Definition at line 66 of file src/QualityMetric/DFT/RI_DFT.hpp.
|
virtual |
Virtual function that computes the gradient of the QualityMetric analytically. The base class implementation of this function simply prints a warning and calls compute_numerical_gradient to calculate the gradient. This is used by metric which mType is ELEMENT_BASED. For parameters, see compute_element_gradient() .
If that function is not over-riden in the concrete class, the base
Parameters description, see QualityMetric::compute_element_gradient() .
Reimplemented from QualityMetric.
Definition at line 1939 of file QualityMetric/DFT/RI_DFT.cpp.
References RI_DFT::a, RI_DFT::b, RI_DFT::c, QualityMetric::compute_element_numerical_gradient(), g_fcn_ridft2(), g_fcn_ridft3(), PatchData::get_barrier_delta(), TargetMatrix::get_cK(), PatchData::get_domain_normal_at_vertex(), PatchData::get_element_index(), MsqMeshEntity::get_element_type(), PatchData::get_vertex_array(), MsqMeshEntity::get_vertex_index_array(), Mesquite::HEXAHEDRON, i, Mesquite::inv(), RI_DFT::invW, j, k, RI_DFT::mAccGrads, RI_DFT::mCoords, RI_DFT::mGrads, RI_DFT::mNormal, Mesquite::MSQ_3RT_2_OVER_6RT_3, MSQ_CHKERR, MSQ_ERRZERO, Mesquite::MSQ_ONE_THIRD, MSQ_SETERR, MsqError::NOT_IMPLEMENTED, Mesquite::QUADRILATERAL, PatchData::targetMatrices, Mesquite::TETRAHEDRON, Mesquite::TRIANGLE, and MsqMeshEntity::vertex_count().

|
virtual |
Virtual function that computes the gradient of the QualityMetric analytically. The base class implementation of this function simply prints a warning and calls compute_numerical_gradient to calculate the gradient. This is used by metric which mType is ELEMENT_BASED. For parameters, see compute_element_gradient() .
If that function is not over-riden in the concrete class, the base
Parameters description, see QualityMetric::compute_element_gradient() .
Reimplemented from QualityMetric.
|
virtual |
If that function is not over-riden in the concrete class, the base class function makes it default to a numerical hessian.
For parameters description, see QualityMetric::compute_element_hessian() .
Reimplemented from QualityMetric.
|
virtual |
If that function is not over-riden in the concrete class, the base class function makes it default to a numerical hessian.
For parameters description, see QualityMetric::compute_element_hessian() .
Reimplemented from QualityMetric.
Definition at line 2179 of file QualityMetric/DFT/RI_DFT.cpp.
References RI_DFT::a, RI_DFT::b, RI_DFT::c, QualityMetric::compute_element_numerical_hessian(), PatchData::get_barrier_delta(), TargetMatrix::get_cK(), PatchData::get_domain_normal_at_vertex(), PatchData::get_element_index(), MsqMeshEntity::get_element_type(), PatchData::get_vertex_array(), MsqMeshEntity::get_vertex_index_array(), h_fcn_ridft2(), h_fcn_ridft3(), Mesquite::HEXAHEDRON, i, Mesquite::inv(), RI_DFT::invW, j, k, RI_DFT::mCoords, RI_DFT::mGrads, RI_DFT::mHessians, RI_DFT::mNormal, Mesquite::MSQ_3RT_2_OVER_6RT_3, MSQ_CHKERR, MSQ_ERRZERO, Mesquite::MSQ_ONE_THIRD, MSQ_SETERR, MsqError::NOT_IMPLEMENTED, Mesquite::QUADRILATERAL, PatchData::targetMatrices, Mesquite::TETRAHEDRON, Mesquite::transpose(), Mesquite::TRIANGLE, MsqMeshEntity::vertex_count(), and Matrix3D::zero().

|
virtual |
Evaluate the metric for an element.
Reimplemented from QualityMetric.
|
virtual |
Evaluate the metric for an element.
Reimplemented from QualityMetric.
Definition at line 1812 of file QualityMetric/DFT/RI_DFT.cpp.
References RI_DFT::a, RI_DFT::b, RI_DFT::c, PatchData::get_barrier_delta(), TargetMatrix::get_cK(), PatchData::get_domain_normal_at_vertex(), PatchData::get_element_index(), MsqMeshEntity::get_element_type(), PatchData::get_vertex_array(), MsqMeshEntity::get_vertex_index_array(), Mesquite::HEXAHEDRON, i, Mesquite::inv(), RI_DFT::invW, j, Vector3D::length(), m_fcn_ridft2(), m_fcn_ridft3(), RI_DFT::mCoords, RI_DFT::mNormal, Mesquite::MSQ_3RT_2_OVER_6RT_3, MSQ_ERRZERO, Mesquite::MSQ_ONE_THIRD, MSQ_SETERR, Vector3D::normalize(), MsqError::NOT_IMPLEMENTED, Mesquite::QUADRILATERAL, PatchData::targetMatrices, Mesquite::TETRAHEDRON, Mesquite::TRIANGLE, and MsqMeshEntity::vertex_count().

|
private |
Definition at line 94 of file includeLinks/RI_DFT.hpp.
Referenced by RI_DFT::compute_element_analytical_gradient(), RI_DFT::compute_element_analytical_hessian(), and RI_DFT::evaluate_element().
|
private |
Definition at line 95 of file includeLinks/RI_DFT.hpp.
Referenced by RI_DFT::compute_element_analytical_gradient(), RI_DFT::compute_element_analytical_hessian(), and RI_DFT::evaluate_element().
|
private |
Definition at line 96 of file includeLinks/RI_DFT.hpp.
Referenced by RI_DFT::compute_element_analytical_gradient(), RI_DFT::compute_element_analytical_hessian(), and RI_DFT::evaluate_element().
|
private |
Definition at line 104 of file includeLinks/RI_DFT.hpp.
Referenced by RI_DFT::compute_element_analytical_gradient(), RI_DFT::compute_element_analytical_hessian(), and RI_DFT::evaluate_element().
|
private |
Definition at line 102 of file includeLinks/RI_DFT.hpp.
Referenced by RI_DFT::compute_element_analytical_gradient().
|
private |
Definition at line 100 of file includeLinks/RI_DFT.hpp.
Referenced by RI_DFT::compute_element_analytical_gradient(), RI_DFT::compute_element_analytical_hessian(), and RI_DFT::evaluate_element().
|
private |
Definition at line 101 of file includeLinks/RI_DFT.hpp.
Referenced by RI_DFT::compute_element_analytical_gradient(), and RI_DFT::compute_element_analytical_hessian().
|
private |
Definition at line 103 of file includeLinks/RI_DFT.hpp.
Referenced by RI_DFT::compute_element_analytical_hessian().
|
private |
Definition at line 99 of file includeLinks/RI_DFT.hpp.
Referenced by RI_DFT::compute_element_analytical_gradient(), RI_DFT::compute_element_analytical_hessian(), and RI_DFT::evaluate_element().