PlaneS3< FT > Class Template Reference

#include <PlaneS3.h>

Public Member Functions
	PlaneS3 ()
	PlaneS3 (const PointS3< FT > &p, const PointS3< FT > &q, const PointS3< FT > &r)
	PlaneS3 (const PointS3< FT > &p, const DirectionS3< FT > &d)
	PlaneS3 (const PointS3< FT > &p, const VectorS3< FT > &v)
	PlaneS3 (const FT &a, const FT &b, const FT &c, const FT &d)
	PlaneS3 (const LineS3< FT > &l, const PointS3< FT > &p)
	PlaneS3 (const SegmentS3< FT > &s, const PointS3< FT > &p)
	PlaneS3 (RayS3< FT > &r, const PointS3< FT > &p)
bool	operator== (const PlaneS3< FT > &p) const
bool	operator!= (const PlaneS3< FT > &p) const
const FT &	a () const
const FT &	b () const
const FT &	c () const
const FT &	d () const
LineS3< FT >	perpendicular_line (const PointS3< FT > &p) const
PlaneS3	opposite () const
PointS3< FT >	point () const
PointS3< FT >	projection (const PointS3< FT > &p) const
VectorS3< FT >	orthogonal_vector () const
DirectionS3< FT >	orthogonal_direction () const
VectorS3< FT >	base1 () const
VectorS3< FT >	base2 () const
PointS3< FT >	to_plane_basis (const PointS3< FT > &p) const
PointS2< FT >	to_2d (const PointS3< FT > &p) const
PointS3< FT >	to_3d (const PointS2< FT > &p) const
PlaneS3	transform (const Aff_transformationS3< FT > &t) const
Oriented_side	oriented_side (const PointS3< FT > &p) const
bool	has_on_boundary (const PointS3< FT > &p) const
bool	has_on_boundary (const LineS3< FT > &p) const
bool	has_on_positive_side (const PointS3< FT > &l) const
bool	has_on_negative_side (const PointS3< FT > &l) const
bool	is_degenerate () const
void	new_rep (const PointS3< FT > &p, const PointS3< FT > &q, const PointS3< FT > &r)
void	new_rep (const FT &a, const FT &b, const FT &c, const FT &d)

Public Attributes
FT	e0
FT	e1
FT	e2
FT	e3

Detailed Description

template<class FT>
class PlaneS3< FT >

Definition at line 61 of file PlaneS3.h.

Constructor & Destructor Documentation

PlaneS3 ( )

inline

Definition at line 64 of file PlaneS3.h.

{}

CGAL_END_NAMESPACE CGAL_BEGIN_NAMESPACE PlaneS3	(	const PointS3< FT > &	p,
		const PointS3< FT > &	q,
		const PointS3< FT > &	r
	)

Definition at line 169 of file PlaneS3.h.

{ new_rep(p, q, r); }

PlaneS3	(	const PointS3< FT > &	p,
		const DirectionS3< FT > &	d
	)

Definition at line 175 of file PlaneS3.h.

References DirectionS3< FT >::dx(), DirectionS3< FT >::dy(), DirectionS3< FT >::dz(), PointS3< FT >::x(), PointS3< FT >::y(), and PointS3< FT >::z().

{
  new_rep(d.dx(), d.dy(),
          d.dz(),
          -d.dx() * p.x() - d.dy() * p.y() - d.dz() * p.z());
}

Here is the call graph for this function:

PlaneS3	(	const PointS3< FT > &	p,
		const VectorS3< FT > &	v
	)

Definition at line 183 of file PlaneS3.h.

References VectorS3< FT >::x(), PointS3< FT >::x(), VectorS3< FT >::y(), PointS3< FT >::y(), VectorS3< FT >::z(), and PointS3< FT >::z().

{ new_rep(v.x(), v.y(), v.z(), -v.x() * p.x() - v.y() * p.y() - v.z() * p.z()); }

Here is the call graph for this function:

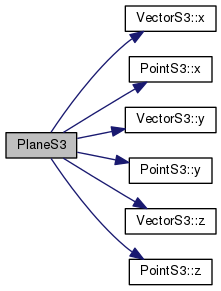
PlaneS3	(	const FT &	a,
		const FT &	b,
		const FT &	c,
		const FT &	d
	)

Definition at line 187 of file PlaneS3.h.

{ new_rep(a, b, c, d); }

PlaneS3	(	const LineS3< FT > &	l,
		const PointS3< FT > &	p
	)

Definition at line 191 of file PlaneS3.h.

References LineS3< FT >::direction(), and LineS3< FT >::point().

{ new_rep(l.point(), l.point()+l.direction().vector(), p); }

Here is the call graph for this function:

PlaneS3	(	const SegmentS3< FT > &	s,
		const PointS3< FT > &	p
	)

Definition at line 195 of file PlaneS3.h.

References SegmentS3< FT >::end(), and SegmentS3< FT >::start().

{ new_rep(s.start(), s.end(), p); }

Here is the call graph for this function:

PlaneS3	(	RayS3< FT > &	r,
		const PointS3< FT > &	p
	)

Definition at line 199 of file PlaneS3.h.

References RayS3< FT >::second_point(), and RayS3< FT >::start().

{ new_rep(r.start(), r.second_point(), p); }

Here is the call graph for this function:

Member Function Documentation

const FT & a

(

)

const

Definition at line 219 of file PlaneS3.h.

Referenced by cmp_signed_dist_to_plane(), gp_linear_intersection(), has_larger_signed_dist_to_plane(), has_smaller_signed_dist_to_plane(), projection(), and scaled_distance_to_plane().

{ return e0; }

Here is the caller graph for this function:

const FT & b

(

)

const

Definition at line 224 of file PlaneS3.h.

Referenced by cmp_signed_dist_to_plane(), gp_linear_intersection(), has_larger_signed_dist_to_plane(), has_smaller_signed_dist_to_plane(), projection(), and scaled_distance_to_plane().

{ return e1; }

Here is the caller graph for this function:

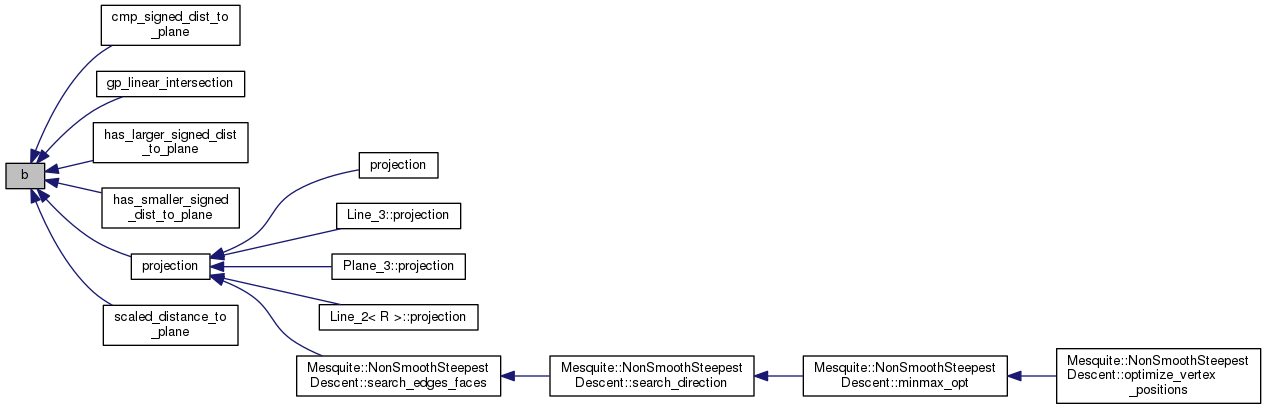
VectorS3< FT > base1

(

)

const

Definition at line 269 of file PlaneS3.h.

{
  if( a() == FT(0) )  // parallel to x-axis
      return VectorS3<FT>(FT(1), FT(0), FT(0));

  if( b() == FT(0) )  // parallel to y-axis
      return VectorS3<FT>(FT(0), FT(1), FT(0));

  if (c() == FT(0) )  // parallel to z-axis
      return VectorS3<FT>(FT(0), FT(0), FT(1));

  return VectorS3<FT>(-b(), a(), FT(0));
}

VectorS3< FT > base2

(

)

const

Definition at line 285 of file PlaneS3.h.

{
  if ( a() == FT(0) ) // parallel to x-axis  x-axis already returned in base1
    {
      if (b() == FT(0) )  // parallel to y-axis
          return VectorS3<FT>(FT(0), FT(1), FT(0));

      if (c() == FT(0) ) // parallel to z-axis
          return VectorS3<FT>(FT(0), FT(0), FT(1));

      return VectorS3<FT>(FT(0), -b(), c());
    }
  if (b() == FT(0) )
      return VectorS3<FT>(c(), FT(0), -a());

  if (c() == FT(0) )
      return VectorS3<FT>(-b(), a(), FT(0));

  return VectorS3<FT>(FT(0), -c(), b());
}

const FT & c

(

)

const

Definition at line 229 of file PlaneS3.h.

Referenced by cmp_signed_dist_to_plane(), gp_linear_intersection(), has_larger_signed_dist_to_plane(), has_smaller_signed_dist_to_plane(), projection(), and scaled_distance_to_plane().

{ return e2; }

Here is the caller graph for this function:

const FT & d

(

)

const

Definition at line 234 of file PlaneS3.h.

Referenced by gp_linear_intersection(), projection(), and scaled_distance_to_plane().

{ return e3; }

Here is the caller graph for this function:

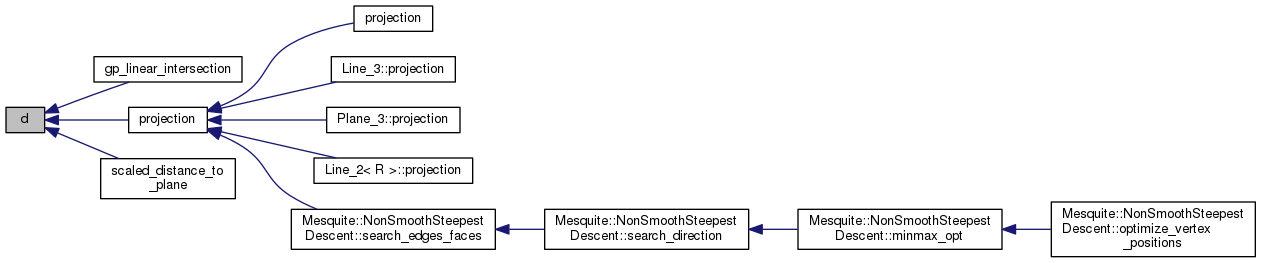
bool has_on_boundary

(

const PointS3< FT > &

p

)

const

Definition at line 380 of file PlaneS3.h.

References d, PointS3< FT >::x(), PointS3< FT >::y(), and PointS3< FT >::z().

{
  return (a()*p.x() + b()*p.y() + c()*p.z() +d()) == FT(0);
}

Here is the call graph for this function:

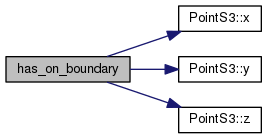
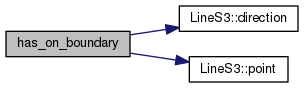
bool has_on_boundary

(

const LineS3< FT > &

p

)

const

Definition at line 386 of file PlaneS3.h.

References LineS3< FT >::direction(), and LineS3< FT >::point().

{
  return has_on_boundary(l.point())
         &&  has_on_boundary(l.point() + l.direction().vector());
}

Here is the call graph for this function:

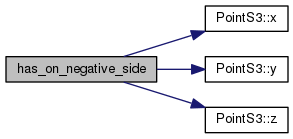
bool has_on_negative_side

(

const PointS3< FT > &

l

)

const

Definition at line 399 of file PlaneS3.h.

References d, PointS3< FT >::x(), PointS3< FT >::y(), and PointS3< FT >::z().

{
  return (a()*p.x() + b()*p.y() + c()*p.z() +d()) < FT(0);
}

Here is the call graph for this function:

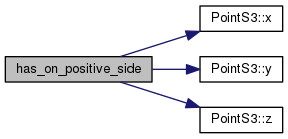
bool has_on_positive_side

(

const PointS3< FT > &

l

)

const

Definition at line 393 of file PlaneS3.h.

References d, PointS3< FT >::x(), PointS3< FT >::y(), and PointS3< FT >::z().

{
  return (a()*p.x() + b()*p.y() + c()*p.z() +d()) > FT(0);
}

Here is the call graph for this function:

bool is_degenerate

(

)

const

Definition at line 406 of file PlaneS3.h.

{
  return (a() == FT(0)) && (b() == FT(0)) && (c() == FT(0));
}

void new_rep ( const PointS3< FT > &  p, const PointS3< FT > &  q, const PointS3< FT > &  r  )

inline

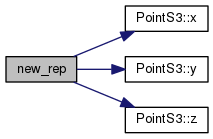
Definition at line 143 of file PlaneS3.h.

References PointS3< FT >::x(), PointS3< FT >::y(), and PointS3< FT >::z().

{
  FT rpx = p.x()-r.x();
  FT rpy = p.y()-r.y();
  FT rpz = p.z()-r.z();
  FT rqx = q.x()-r.x();
  FT rqy = q.y()-r.y();
  FT rqz = q.z()-r.z();
  // Cross product rp * rq.
  e0 = rpy*rqz - rqy*rpz;
  e1 = rpz*rqx - rqz*rpx;
  e2 = rpx*rqy - rqx*rpy;
  e3 = - e0*r.x() - e1*r.y() - e2*r.z();
}

Here is the call graph for this function:

void new_rep ( const FT &  a, const FT &  b, const FT &  c, const FT &  d  )

inline

Definition at line 132 of file PlaneS3.h.

References d.

{
  e0 = a;
  e1 = b;
  e2 = c;
  e3 = d;
}

bool operator!=

(

const PlaneS3< FT > &

p

)

const

Definition at line 212 of file PlaneS3.h.

{
  return !(*this == p);
}

bool operator==

(

const PlaneS3< FT > &

p

)

const

Definition at line 204 of file PlaneS3.h.

References PlaneS3< FT >::orthogonal_direction(), and PlaneS3< FT >::point().

{
  return has_on_boundary(p.point()) &&
         (orthogonal_direction() == p.orthogonal_direction());

}

Here is the call graph for this function:

PlaneS3< FT > opposite

(

)

const

Definition at line 356 of file PlaneS3.h.

References d.

{ return PlaneS3<FT>(-a(),-b(),-c(),-d()); }

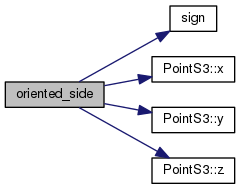
Oriented_side oriented_side

(

const PointS3< FT > &

p

)

const

Definition at line 376 of file PlaneS3.h.

References CGAL_NTS, d, sign(), PointS3< FT >::x(), PointS3< FT >::y(), and PointS3< FT >::z().

{ return Oriented_side(CGAL_NTS sign(a()*p.x() + b()*p.y() + c()*p.z() +d())); }

Here is the call graph for this function:

DirectionS3< FT > orthogonal_direction

(

)

const

Definition at line 263 of file PlaneS3.h.

Referenced by PlaneS3< FT >::operator==().

{
  return DirectionS3<FT>(a(), b(), c());
}

Here is the caller graph for this function:

VectorS3< FT > orthogonal_vector

(

)

const

Definition at line 256 of file PlaneS3.h.

{
  return VectorS3<FT>(a(), b(), c());
}

LineS3< FT > perpendicular_line

(

const PointS3< FT > &

p

)

const

Definition at line 351 of file PlaneS3.h.

{ return LineS3<FT>(p, orthogonal_direction()); }

PointS3< FT > point

(

)

const

Definition at line 238 of file PlaneS3.h.

References d.

Referenced by PlaneS3< FT >::operator==().

{
  if (a() != FT(0)) // not parallel to x-axis
    return PointS3<FT>(-d()/a(), FT(0), FT(0));
  if (b() != FT(0)) // not parallel to y-axis
    return PointS3<FT>(FT(0), -d()/b(), FT(0));
  // parallel to xy-plane => intersects z-axis
  return PointS3<FT>(FT(0), FT(0), -d()/c());
}

Here is the caller graph for this function:

PointS3< FT > projection

(

const PointS3< FT > &

p

)

const

Definition at line 250 of file PlaneS3.h.

References projection().

{
  return CGAL::projection(p, *this);
}

Here is the call graph for this function:

PointS2< FT > to_2d

(

const PointS3< FT > &

p

)

const

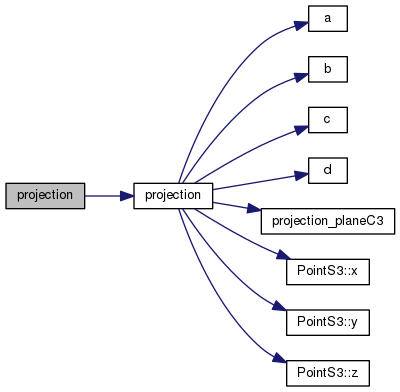
Definition at line 324 of file PlaneS3.h.

References solve(), VectorS3< FT >::x(), VectorS3< FT >::y(), and VectorS3< FT >::z().

{
  const VectorS3<FT>& v0 = base1();
  const VectorS3<FT>& v1 = base2();
  VectorS3<FT> v2 = orthogonal_vector();
  VectorS3<FT> v3 = p - point();
  FT alpha, beta, gamma;

  solve(v0.x(), v0.y(), v0.z(),
        v1.x(), v1.y(), v1.z(),
        v2.x(), v2.y(), v2.z(),
        v3.x(), v3.y(), v3.z(),
        alpha, beta, gamma);

  return PointS2<FT>(alpha, beta);
}

Here is the call graph for this function:

PointS3< FT > to_3d

(

const PointS2< FT > &

p

)

const

Definition at line 343 of file PlaneS3.h.

References PointS2< FT >::x(), and PointS2< FT >::y().

{
  VectorS3<FT> e1 = base1(),
               e2 = base2();
  return point() + p.x() * e1 + p.y() * e2;
}

Here is the call graph for this function:

PointS3< FT > to_plane_basis

(

const PointS3< FT > &

p

)

const

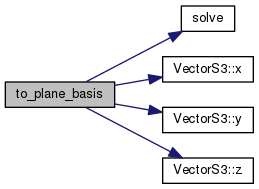
Definition at line 306 of file PlaneS3.h.

References solve(), VectorS3< FT >::x(), VectorS3< FT >::y(), and VectorS3< FT >::z().

{
  const VectorS3<FT>& v0 = base1();
  const VectorS3<FT>& v1 = base2();
  VectorS3<FT> v2 = orthogonal_vector();
  VectorS3<FT> v3 = p - point();
  FT alpha, beta, gamma;

  solve(v0.x(), v0.y(), v0.z(),
        v1.x(), v1.y(), v1.z(),
        v2.x(), v2.y(), v2.z(),
        v3.x(), v3.y(), v3.z(),
        alpha, beta, gamma);

  return PointS3<FT>(alpha, beta, gamma);
}

Here is the call graph for this function:

PlaneS3< FT > transform

(

const Aff_transformationS3< FT > &

t

)

const

Definition at line 361 of file PlaneS3.h.

References Aff_transformationS3< FT >::is_even(), Aff_transformationS3< FT >::transform(), and Aff_transformationS3< FT >::transpose().

Referenced by Aff_transformationS3< FT >::transform().

{
  DirectionS3<FT> dir = t.transpose().inverse().transform(orthogonal_direction());
  if (!t.is_even())  dir = -dir;
  return PlaneS3<FT>( t.transform(point()), dir);
  
/*
  return PlaneS3<FT>( t.transform(point()), (t.is_even())
           ?   t.transpose().inverse().transform(orthogonal_direction())
           : - t.transpose().inverse().transform(orthogonal_direction()) );
*/
}

Here is the call graph for this function:

Here is the caller graph for this function:

Member Data Documentation

FT e0

Definition at line 122 of file PlaneS3.h.

FT e1

Definition at line 123 of file PlaneS3.h.

FT e2

Definition at line 124 of file PlaneS3.h.

FT e3

Definition at line 125 of file PlaneS3.h.

---

The documentation for this class was generated from the following file:

• PlaneS3.h