Rocstar  1.0
Rocstar multiphysics simulation application
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
Public Member Functions | Protected Member Functions | Protected Attributes | Friends | List of all members
Alg_Metric_Base_3 Class Reference

3D Algebraic Metric Base Class More...

#include <Algebraic_Metrics_3.h>

Inheritance diagram for Alg_Metric_Base_3:
Inheritance graph
[legend]
Collaboration diagram for Alg_Metric_Base_3:
Collaboration graph
[legend]

Public Member Functions

 Alg_Metric_Base_3 ()
 Constructor. More...
 
virtual ~Alg_Metric_Base_3 ()
 Virtual Destructor. More...
 
virtual void initialize (Vector_3< double > n[], int type)
 Initialize a 3D Algebraic Metric. More...
 
virtual void initialize (Element_node_enumerator &ene)
 
virtual double maxValue () const
 The maximum value for this metric. More...
 
virtual double minValue () const
 The minimum value for this metric. More...
 
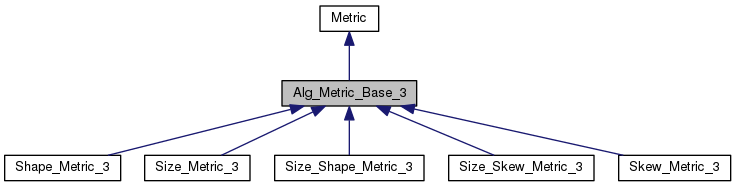
- Public Member Functions inherited from Metric
 Metric ()
 
virtual ~Metric ()
 
virtual void compute (double atts[]) const =0
 Compute the value of this metric. More...
 

Protected Member Functions

double compute_size (double ref_voume=1.) const
 Compute the size metric. More...
 
double compute_shape () const
 Compute the shape metric. More...
 
double compute_skew () const
 Compute the skew metric. More...
 

Protected Attributes

double alpha [8]
 
J_Matrix A [8]
 
Matrix L [8]
 
int type_
 

Friends

std::ostream & operator<< (std::ostream &, const Alg_Metric_Base_3 &)
 

Detailed Description

3D Algebraic Metric Base Class

This class is the base class for the implementation of the specific 3D algebraic metrics defined by Patrick Knupp in "Aglebraic Mesh Quality Metrics for Unstructured Initial Meshes"

Definition at line 42 of file Algebraic_Metrics_3.h.

Constructor & Destructor Documentation

Alg_Metric_Base_3 ( )
inline

Constructor.

Definition at line 48 of file Algebraic_Metrics_3.h.

48 {}
virtual ~Alg_Metric_Base_3 ( )
inlinevirtual

Virtual Destructor.

Although the destructor does nothing, this member function must be declared since the class has other virtual functions.

Definition at line 55 of file Algebraic_Metrics_3.h.

55 {}

Member Function Documentation

double compute_shape ( ) const
protected

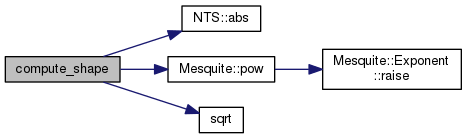
Compute the shape metric.

Definition at line 141 of file Algebraic_Metrics_3.C.

References NTS::abs(), denom, i, Mesquite::pow(), and sqrt().

141  {
142  if (type_ == COM::Connectivity::TET4){
143  double num = (3.0 * pow(alpha[0]*sqrt(2.0),(2.0/3.0)) );
144  double denom = 1.5*(L[0](0,0)+L[0](1,1)+L[0](2,2))-
145  (L[0](0,1)+L[0](1,2)+L[0](0,2));
146  return num/denom;
147  }
148  else{
149  assert (type_ == COM::Connectivity::HEX8);
150  double denom = 0;
151  for (int i = 0; i < 8; i ++){
152  denom += (L[i](0,0) + L[i](1,1) + L[i](2,2))/(pow(abs(alpha[i]),(2.0/3.0)));
153  }
154  return 24.0/denom;
155  }
156 }
sqrt
double sqrt(double d)
Definition: double.h:73
Alg_Metric_Base_3::L
Matrix L[8]
Definition: Algebraic_Metrics_3.h:89
Alg_Metric_Base_3::alpha
double alpha[8]
Definition: Algebraic_Metrics_3.h:87
i
blockLoc i
Definition: read.cpp:79
NTS::abs
NT abs(const NT &x)
Definition: number_utils.h:130
Alg_Metric_Base_3::type_
int type_
Definition: Algebraic_Metrics_3.h:90
Mesquite::pow
double pow(double value, const Exponent &exp)
Definition: includeLinks/Exponent.hpp:89
denom
CGAL_BEGIN_NAMESPACE void const NT NT NT NT & denom
Definition: rational_rotation.h:61

Here is the call graph for this function:

double compute_size ( double  ref_voume = 1.) const
protected

Compute the size metric.

Parameters
ref_areathe ideal area for this element.

Definition at line 122 of file Algebraic_Metrics_3.C.

References i.

122  {
123  double size = 0.0;
124  if (type_ == COM::Connectivity::TET4){
125  size = (alpha[0]/6.0)/ref_vol;
126  size = (size < (1/size))? size : (1/size);
127  }
128  if (type_ == COM::Connectivity::HEX8){
129  for (int i = 0; i < 8; i++){
130  size += alpha[i];
131  }
132  if (size < 0) {size = 0;}
133  else {
134  size = size / ( 8.0 * ref_vol );
135  size = (size < (1/size))? size: (1/size);
136  }
137  }
138  return size;
139 }
Alg_Metric_Base_3::alpha
double alpha[8]
Definition: Algebraic_Metrics_3.h:87
i
blockLoc i
Definition: read.cpp:79
Alg_Metric_Base_3::type_
int type_
Definition: Algebraic_Metrics_3.h:90
double compute_skew ( ) const
protected

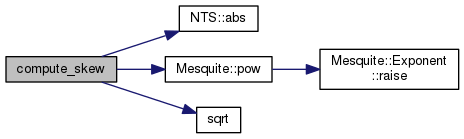
Compute the skew metric.

Definition at line 158 of file Algebraic_Metrics_3.C.

References NTS::abs(), denom, i, Mesquite::pow(), and sqrt().

158  {
159  // Not defined for Tets, so we return 1
160  if (type_ == COM::Connectivity::TET4) {
161  return 1.0;
162  }
163 
164  // For quads, set flag in case of divide by zero (degenerate element)
165  else{
166  assert (type_ == COM::Connectivity::HEX8);
167  double denom = 0.0;
168  int flag = 0;
169  for (int i = 0; i < 8; i ++){
170  double root = sqrt(L[i](0,0)*L[i](1,1)*L[i](2,2));
171  if (root == 0) { flag = 1;}
172  denom += pow( abs(root/alpha[i]), (2.0/3.0));
173  }
174  if (flag) { return 0.0;}
175  else { return 8.0/denom; }
176  }
177 }
sqrt
double sqrt(double d)
Definition: double.h:73
Alg_Metric_Base_3::L
Matrix L[8]
Definition: Algebraic_Metrics_3.h:89
Alg_Metric_Base_3::alpha
double alpha[8]
Definition: Algebraic_Metrics_3.h:87
i
blockLoc i
Definition: read.cpp:79
NTS::abs
NT abs(const NT &x)
Definition: number_utils.h:130
Alg_Metric_Base_3::type_
int type_
Definition: Algebraic_Metrics_3.h:90
Mesquite::pow
double pow(double value, const Exponent &exp)
Definition: includeLinks/Exponent.hpp:89
denom
CGAL_BEGIN_NAMESPACE void const NT NT NT NT & denom
Definition: rational_rotation.h:61

Here is the call graph for this function:

void initialize ( Vector_3< double >  n[],
int  type 
)
virtual

Initialize a 3D Algebraic Metric.

Parameters
n[]Ordered set of nodal coordinates.
typeElement type: TET or QUAD

Implements Metric.

Definition at line 82 of file Algebraic_Metrics_3.C.

References A, i, j, and v.

Referenced by main().

82  {
83  type_ = type;
84  vector<Vector_3<double> > v(3);
85  if (type_ == COM::Connectivity::TET4){
86  double premult = 1.0;
87  for ( int i = 0; i < 4; i ++){
88  for (int j = 0; j < 3; j ++){
89  v[0][j] = premult * (n[(i+1)%4][j] - n[i][j]);
90  v[1][j] = premult * (n[(i+2)%4][j] - n[i][j]);
91  v[2][j] = premult * (n[(i+3)%4][j] - n[i][j]);
92  }
93  A[i] = J_Matrix(&v[0],3);
94  L[i] ^= A[i];
95  alpha[i] = A[i].det();
96  premult *= -1.0;
97  }
98  }
99  else if (type_ == COM::Connectivity::HEX8){
100  double premult = 1.0;
101  for ( int i = 0; i < 8; i ++){
102 
103  if ( (i==0) || (i==3) || (i==5) || (i==6) ) { premult = 1.0; }
104  else if ( (i==1) || (i==2) || (i==4) || (i==7) ) { premult = -1.0; }
105  int a,b,c;
106  if ( (i == 0) || (i == 4) ) { a=1; b=3; c=4; }
107  else if ( (i ==3) || (i==7) ) { a=4;b=5;c=7; }
108  else {a=1;b=4;c=7;}
109 
110  for (int j = 0; j < 3; j ++){
111  v[0][j] = premult*( n[(i+a)%8][j] - n[i][j]);
112  v[1][j] = premult*( n[(i+b)%8][j] - n[i][j]);
113  v[2][j] = premult*( n[(i+c)%8][j] - n[i][j]);
114  }
115  A[i] = J_Matrix(&v[0],3);
116  L[i] ^= A[i];
117  alpha[i] = A[i].det();
118  }
119  }
120 }
v
*********************************************************************Illinois Open Source License ****University of Illinois NCSA **Open Source License University of Illinois All rights reserved ****Developed free of to any person **obtaining a copy of this software and associated documentation to deal with the Software without including without limitation the rights to and or **sell copies of the and to permit persons to whom the **Software is furnished to do subject to the following this list of conditions and the following disclaimers ****Redistributions in binary form must reproduce the above **copyright this list of conditions and the following **disclaimers in the documentation and or other materials **provided with the distribution ****Neither the names of the Center for Simulation of Advanced the University of nor the names of its **contributors may be used to endorse or promote products derived **from this Software without specific prior written permission ****THE SOFTWARE IS PROVIDED AS WITHOUT WARRANTY OF ANY **EXPRESS OR INCLUDING BUT NOT LIMITED TO THE WARRANTIES **OF FITNESS FOR A PARTICULAR PURPOSE AND **NONINFRINGEMENT IN NO EVENT SHALL THE CONTRIBUTORS OR **COPYRIGHT HOLDERS BE LIABLE FOR ANY DAMAGES OR OTHER WHETHER IN AN ACTION OF TORT OR **ARISING OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE **USE OR OTHER DEALINGS WITH THE SOFTWARE v
Definition: roccomf90.h:20
Alg_Metric_Base_3::L
Matrix L[8]
Definition: Algebraic_Metrics_3.h:89
Alg_Metric_Base_3::alpha
double alpha[8]
Definition: Algebraic_Metrics_3.h:87
i
blockLoc i
Definition: read.cpp:79
j
j indices j
Definition: Indexing.h:6
Alg_Metric_Base_3::A
J_Matrix A[8]
Definition: Algebraic_Metrics_3.h:88
Alg_Metric_Base_3::type_
int type_
Definition: Algebraic_Metrics_3.h:90

Here is the caller graph for this function:

void initialize ( Element_node_enumerator &  ene)
virtual

Implements Metric.

Definition at line 40 of file Algebraic_Metrics_3.C.

References A, i, j, n, and v.

40  {
41  type_ = ene.type();
42  Element_node_vectors_k_const<double> n;
43  n.set(ene.pane()->attribute("nc"),ene);
44  vector<Vector_3<double> > v(2);
45  if (type_ == COM::Connectivity::TET4){
46  double premult = 1.0;
47  for ( int i = 0; i < 4; i ++){
48  for (int j = 0; j < 3; j ++){
49  v[0][j] = premult * (n((i+1)%4,j) - n(i,j));
50  v[1][j] = premult * (n((i+2)%4,j) - n(i,j));
51  v[2][j] = premult * (n((i+3)%4,j) - n(i,j));
52  }
53  A[i] = J_Matrix(&v[0],3);
54  L[i] ^= A[i];
55  alpha[i] = A[i].det();
56  premult *= -1.0;
57  }
58  }
59  else if (type_ == COM::Connectivity::HEX8){
60  double premult = 1.0;
61  for ( int i = 0; i < 8; i ++){
62 
63  if ( (i==0) || (i==3) || (i==5) || (i==6) ) { premult = 1.0; }
64  else if ( (i==1) || (i==2) || (i==4) || (i==7) ) { premult = -1.0; }
65  int a,b,c;
66  if ( (i == 0) || (i == 4) ) { a=1; b=3; c=4; }
67  else if ( (i ==3) || (i==7) ) { a=4;b=5;c=7; }
68  else {a=1;b=4;c=7;}
69 
70  for (int j = 0; j < 3; j ++){
71  v[0][j] = premult*( n((i+a)%8,j) - n(i,j));
72  v[1][j] = premult*( n((i+b)%8,j) - n(i,j));
73  v[2][j] = premult*( n((i+c)%8,j) - n(i,j));
74  }
75  A[i] = J_Matrix(&v[0],3);
76  L[i] ^= A[i];
77  alpha[i] = A[i].det();
78  }
79  }
80 }
v
*********************************************************************Illinois Open Source License ****University of Illinois NCSA **Open Source License University of Illinois All rights reserved ****Developed free of to any person **obtaining a copy of this software and associated documentation to deal with the Software without including without limitation the rights to and or **sell copies of the and to permit persons to whom the **Software is furnished to do subject to the following this list of conditions and the following disclaimers ****Redistributions in binary form must reproduce the above **copyright this list of conditions and the following **disclaimers in the documentation and or other materials **provided with the distribution ****Neither the names of the Center for Simulation of Advanced the University of nor the names of its **contributors may be used to endorse or promote products derived **from this Software without specific prior written permission ****THE SOFTWARE IS PROVIDED AS WITHOUT WARRANTY OF ANY **EXPRESS OR INCLUDING BUT NOT LIMITED TO THE WARRANTIES **OF FITNESS FOR A PARTICULAR PURPOSE AND **NONINFRINGEMENT IN NO EVENT SHALL THE CONTRIBUTORS OR **COPYRIGHT HOLDERS BE LIABLE FOR ANY DAMAGES OR OTHER WHETHER IN AN ACTION OF TORT OR **ARISING OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE **USE OR OTHER DEALINGS WITH THE SOFTWARE v
Definition: roccomf90.h:20
Alg_Metric_Base_3::L
Matrix L[8]
Definition: Algebraic_Metrics_3.h:89
Alg_Metric_Base_3::alpha
double alpha[8]
Definition: Algebraic_Metrics_3.h:87
i
blockLoc i
Definition: read.cpp:79
n
const NT & n
Definition: rational_rotation.h:72
j
j indices j
Definition: Indexing.h:6
Alg_Metric_Base_3::A
J_Matrix A[8]
Definition: Algebraic_Metrics_3.h:88
Alg_Metric_Base_3::type_
int type_
Definition: Algebraic_Metrics_3.h:90
virtual double maxValue ( ) const
inlinevirtual

The maximum value for this metric.

Implements Metric.

Definition at line 67 of file Algebraic_Metrics_3.h.

Referenced by main().

67 { return 1.0; }

Here is the caller graph for this function:

virtual double minValue ( ) const
inlinevirtual

The minimum value for this metric.

Implements Metric.

Definition at line 70 of file Algebraic_Metrics_3.h.

Referenced by main().

70 { return 0.0; }

Here is the caller graph for this function:

Friends And Related Function Documentation

std::ostream& operator<< ( std::ostream &  output,
const Alg_Metric_Base_3 &  m 
)
friend

Definition at line 199 of file Algebraic_Metrics_3.C.

199  {
200  for(int i =0; i < (m.type_-100); i ++){
201  output << "A[" << i << "]:" << endl << m.A[i];
202  output << "L[" << i << "]:" << endl << m.L[i];
203  output << "alpha"<<i << ": " << m.alpha[i] << endl << endl;
204  }
205  return output;
206 }
Alg_Metric_Base_3::L
Matrix L[8]
Definition: Algebraic_Metrics_3.h:89
Alg_Metric_Base_3::alpha
double alpha[8]
Definition: Algebraic_Metrics_3.h:87
i
blockLoc i
Definition: read.cpp:79
Alg_Metric_Base_3::A
J_Matrix A[8]
Definition: Algebraic_Metrics_3.h:88
Alg_Metric_Base_3::type_
int type_
Definition: Algebraic_Metrics_3.h:90

Member Data Documentation

J_Matrix A[8]
protected

Definition at line 88 of file Algebraic_Metrics_3.h.

Referenced by operator<<().

double alpha[8]
protected

Definition at line 87 of file Algebraic_Metrics_3.h.

Referenced by operator<<().

Matrix L[8]
protected

Definition at line 89 of file Algebraic_Metrics_3.h.

Referenced by operator<<().

int type_
protected

Definition at line 90 of file Algebraic_Metrics_3.h.

Referenced by operator<<().

The documentation for this class was generated from the following files: