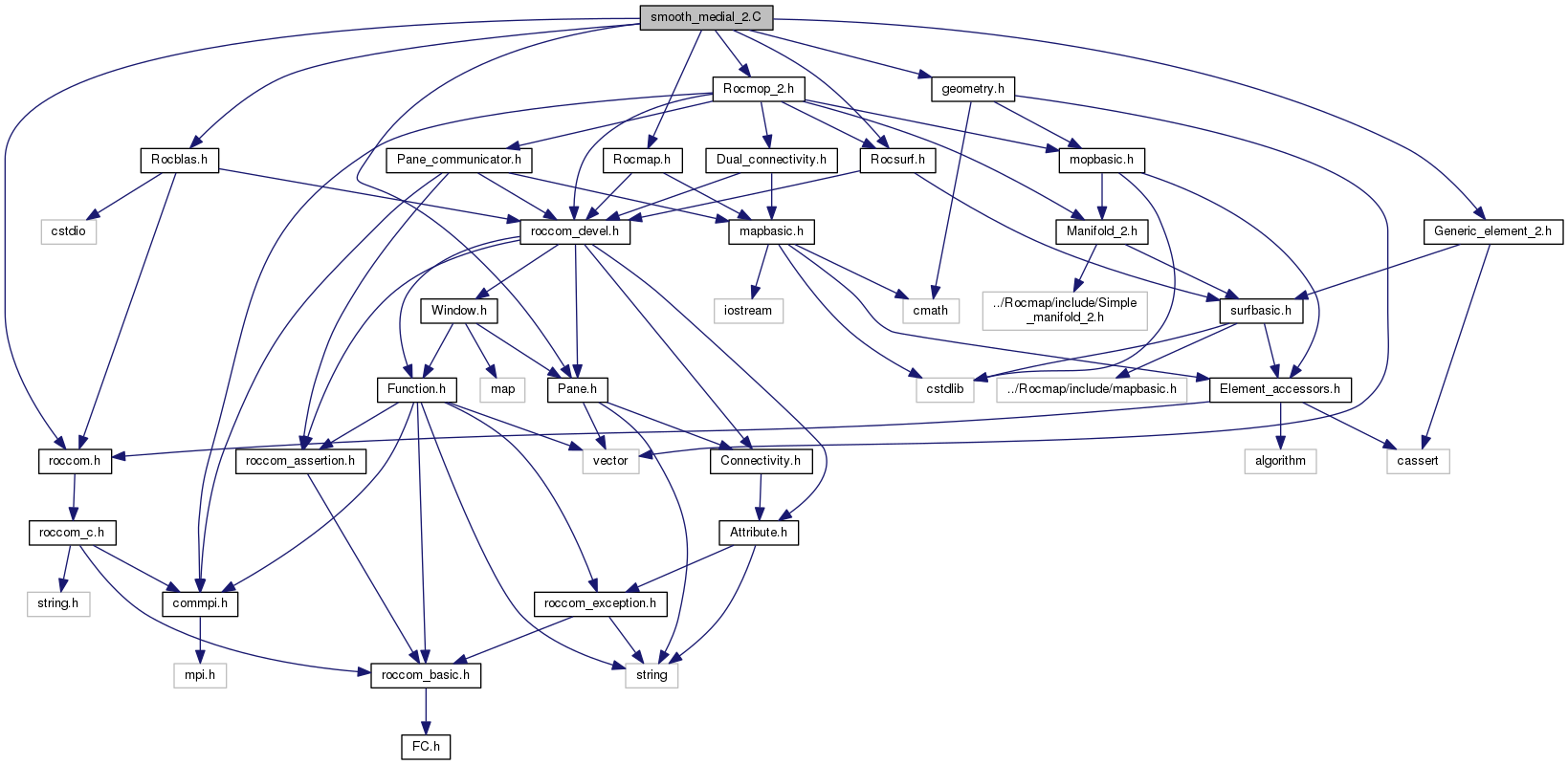
#include "Rocmop_2.h"
#include "roccom.h"
#include "Pane.h"
#include "Rocblas.h"
#include "Rocmap.h"
#include "geometry.h"
#include "Rocsurf.h"
#include "Generic_element_2.h"
Go to the source code of this file.
|
| double | SQR (double x) |
| |
| void | dsytrd3 (double A[3][3], double Q[3][3], double d[3], double e[2]) |
| |
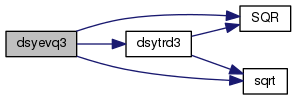
| int | dsyevq3 (double A[3][3], double Q[3][3], double w[3]) |
| |
|
| static const double | half_pi = 1.5707963267949 |
| |
| static const double | pi = 3.14159265358979 |
| |
| #define EXPORT_DEBUG_INFO 1 |
| int dsyevq3 |
( |
double |
A[3][3], |
|
|
double |
Q[3][3], |
|
|
double |
w[3] |
|
) |
| |
Definition at line 124 of file smooth_medial_2.C.
References dsytrd3(), i, k, s, SQR(), and sqrt().
148 double g, r, p, f, b,
s, c, t;
159 for (
int l=0; l < 2; l++)
166 for (m=l; m < 2; m++)
168 g = fabs(w[m])+fabs(w[m+1]);
169 if (fabs(e[m]) + g == g)
179 g = (w[l+1] - w[l]) / (e[l] + e[l]);
182 g = w[m] - w[l] + e[l]/(g + r);
184 g = w[m] - w[l] + e[l]/(g - r);
188 for (
int i=m-1;
i >= l;
i--)
192 if (fabs(f) > fabs(g))
208 r = (w[
i] - g)*s + 2.0*c*b;
214 for (
int k=0;
k < 3;
k++)
217 Q[
k][
i+1] = s*Q[
k][
i] + c*t;
218 Q[
k][
i] = c*Q[
k][
i] - s*t;
| void dsytrd3 |
( |
double |
A[3][3], |
|
|
double |
Q[3][3], |
|
|
double |
d[3], |
|
|
double |
e[2] |
|
) |
| |
Definition at line 48 of file smooth_medial_2.C.
References i, j, q, SQR(), and sqrt().
66 for (
int i=0;
i < 3;
i++)
69 for (
int j=0;
j <
i;
j++)
70 Q[i][
j] = Q[
j][i] = 0.0;
89 for (
int i=1;
i < 3;
i++)
91 f = A[1][
i] * u[1] + A[
i][2] * u[2];
95 K *= 0.5 *
SQR(omega);
97 for (
int i=1;
i < 3;
i++)
98 q[
i] = q[
i] - K * u[
i];
101 d[1] = A[1][1] - 2.0*q[1]*u[1];
102 d[2] = A[2][2] - 2.0*q[2]*u[2];
105 for (
int j=1;
j < 3;
j++)
108 for (
int i=1;
i < 3;
i++)
109 Q[
i][
j] = Q[
i][
j] - f*u[
i];
113 e[1] = A[1][2] - q[1]*u[2] - u[1]*q[2];
117 for (
int i=0;
i < 3;
i++)
| const double half_pi = 1.5707963267949 |
|
static |
| const double pi = 3.14159265358979 |
|
static |