Geo_Metric_Base_3 Class Reference

3D Geometric Metric Base Class More...

#include <Geometric_Metrics_3.h>

Inheritance diagram for Geo_Metric_Base_3:

Collaboration diagram for Geo_Metric_Base_3:

Public Member Functions
	Geo_Metric_Base_3 ()
virtual	~Geo_Metric_Base_3 ()
virtual void	initialize (Vector_3< double > n[], int type)
	Initialize a 3D Geometric Metric by nodal coords and element type. More...
virtual void	initialize (Element_node_enumerator &ene)
	Initialize a 3D Geometric Metric by Element_node_enumerator. More...
virtual double	maxValue () const
	The maximum value for this metric. More...
virtual double	minValue () const
	The minimum value for this metric. More...
Public Member Functions inherited from Metric
	Metric ()
virtual	~Metric ()
virtual void	compute (double atts[]) const =0
	Compute the value of this metric. More...

Protected Member Functions
void	compute_angles (double &min, double &max) const
	Compute min and max dihedral angles. More...
void	compute_aspects (double &R, double &r, double &l) const
	Compute circumradius, inradius, and shortest edge length. More...

Protected Attributes
std::vector< Vector_3< double > >	v
int	_type
const COM::Pane *	_ene_pane
int	_ene_i

Detailed Description

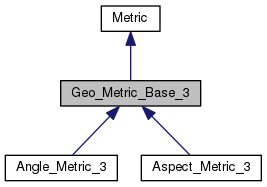
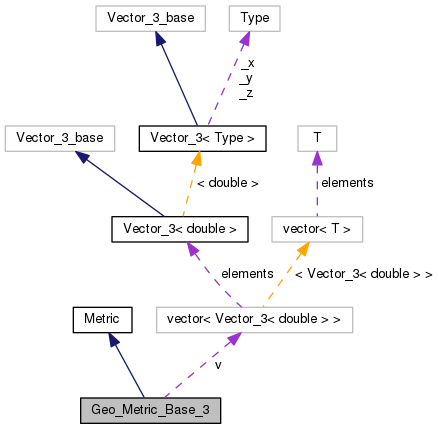
3D Geometric Metric Base Class

This class is the base class for the implementation of various 3D geometric element quality metrics.

Definition at line 43 of file Geometric_Metrics_3.h.

Constructor & Destructor Documentation

Geo_Metric_Base_3 ( )

inline

Definition at line 48 of file Geometric_Metrics_3.h.

: _ene_pane(NULL), _ene_i(0){;}

virtual ~Geo_Metric_Base_3 ( )

inlinevirtual

Definition at line 50 of file Geometric_Metrics_3.h.

{;}

Member Function Documentation

void compute_angles ( double &  min, double &  max  ) const

protected

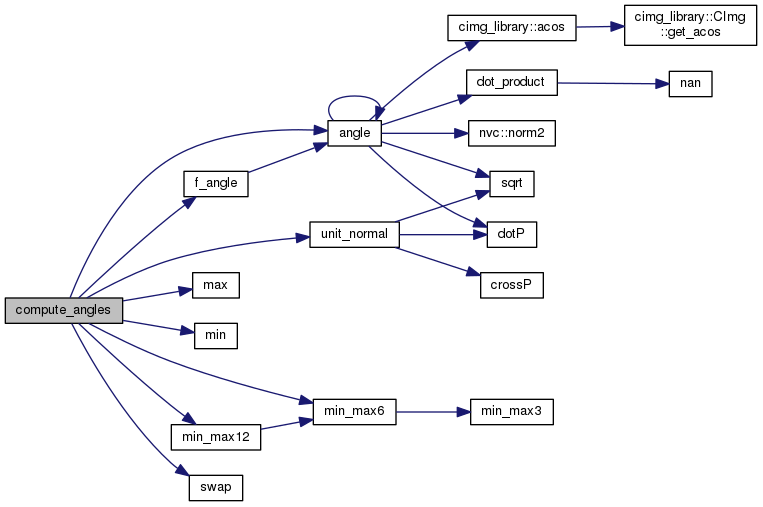
Compute min and max dihedral angles.

Definition at line 100 of file Geometric_Metrics_3.C.

References angle(), f_angle(), i, j, max(), min(), min_max12(), min_max6(), n, ni, nj, swap(), unit_normal(), and v.

                                                                    {
  if (_type == COM::Connectivity::TET4){
    double a12,a13,a14,a23,a24,a34;
    Vector_3<double> n1,n2,n3,n4;
    unit_normal(v[2],v[3],n1); unit_normal(v[5],v[2],n2);
    unit_normal(v[3],v[5],n3); unit_normal(v[0],v[4],n4);
    a12=f_angle(n1,n2); a13=f_angle(n1,n3); a14=f_angle(n1,n4);
    a23=f_angle(n2,n3); a24=f_angle(n2,n4); a34=f_angle(n3,n4);
    min_max6(a12,a13,a14,a23,a24,a34,min,max);
  }
  else if (_type == COM::Connectivity::HEX8){
    double a12,a14,a25,a34,a26,a46,a13,a15,a23,a45,a36,a56;
    Vector_3<double> n1,n2,n3,n4,n5,n6;

    unit_normal(v[1],v[0],n1); unit_normal(v[0],v[4],n2); 
    unit_normal(v[4],v[2],n3); unit_normal(v[3],v[5],n4); 
    unit_normal(v[5],v[1],n5); unit_normal(v[6],v[7],n6);

    a12= f_angle(n1,n2); a13= f_angle(n1,n3); a14= f_angle(n1,n4);
    a15= f_angle(n1,n5); a25= f_angle(n2,n5); a23= f_angle(n2,n3);
    a34= f_angle(n3,n4); a45= f_angle(n4,n5); a26= f_angle(n2,n6); 
    a36= f_angle(n3,n6); a46= f_angle(n4,n6); a56= f_angle(n5,n6);

    min_max12(a12,a15,a34,a36,a13,a25,a45,a46,a14,a23,a26,a56,min,max);
  }
  else {

    const int face_node_lists_pyra[5][8] =
      { {0,3,2,1,8,7,6,5}, {0,1,4,5,10,9,-1,-1}, {1,2,4,6,11,10,-1,-1},
        {2,3,4,7,12,11,-1,-1}, {3,0,4,8,9,12,-1,-1}};
    
    const int face_node_lists_pris[5][9] =
      { {0,1,4,3,6,10,12,9,15}, {1,2,5,4,7,11,13,10,16}, {2,0,3,5,8,9,14,11,17},
        {0,2,1,8,7,6,-1,-1,-1}, {3,4,5,12,13,14,-1,-1,-1}};

    // Create an element node enumerator for handling this element
    Element_node_enumerator ene(_ene_pane, 
                                _ene_i);
    // Loop over faces,
    //     a) determining which share an edge and
    //     b) face normals

    std::vector<Vector_3<double> > fnormals(ene.size_of_faces());
    Element_node_vectors_k_const<double> n;
    n.set(ene.pane()->attribute("nc"),ene);
    // map from edges to faces
    std::map<std::pair<int,int>,int> e2f;
    std::map<std::pair<int,int>,int>::iterator e2f_it;
    // set of adjacent faces
    std::set<std::pair<int,int> > afs;
    std::set<std::pair<int,int> >::iterator afs_it;
    for(int i=0, ni = ene.size_of_faces(); i<ni; ++i){

          Facet_node_enumerator fne( &ene, i);

      const int *fn_list = (_type == COM::Connectivity::PYRIMID5) ? 
        face_node_lists_pyra[i] : face_node_lists_pris[i];

      int i0 = fn_list[0];
      int i1 = fn_list[1];
      int i2 = fn_list[2];

      // Find face normal
      Vector_3<double> e1,e2;
      e1[0] = n(i1,0)-n(i0,0);
      e1[1] = n(i1,1)-n(i0,1);
      e1[2] = n(i1,2)-n(i0,2);
      e2[0] = n(i2,0)-n(i1,0);
      e2[1] = n(i2,1)-n(i1,1);
      e2[2] = n(i2,2)-n(i1,2);
      unit_normal(e1,e2,fnormals[i]);

      for(int j=0, nj = fne.size_of_edges();j<nj;++j){

        // Loop over the edges of this face.
        // If we there is a matching edge, store the adjacent
        // faces.
        int node_id1 = fne[j],node_id2 = fne[(j+1)%nj];
        if(node_id1>node_id2)
          std::swap(node_id1, node_id2);
        e2f_it = e2f.find(std::make_pair<int,int>(node_id1,node_id2));
        if(e2f_it != e2f.end()){
          afs.insert(std::make_pair<int,int>(e2f_it->second,i));
          e2f.erase(e2f_it);
        }
        else{
          e2f.insert(std::make_pair<std::pair<int,int>,int>(
                     std::make_pair<int,int>(node_id1,node_id2)
                     ,i));
        }       
      }
      min = 180.0; max = 0.0;
      for(afs_it = afs.begin(); afs_it != afs.end(); ++afs_it){
        int ind1 = afs_it->first;
        int ind2 = afs_it->second;
        double angle = f_angle(fnormals[ind1],
                               fnormals[ind2]);
        min = (angle < min) ? angle : min;
        max = (angle > max) ? angle : max;
      }
    }
  }
}

Here is the call graph for this function:

void compute_aspects ( double &  R, double &  r, double &  l  ) const

protected

Compute circumradius, inradius, and shortest edge length.

Definition at line 204 of file Geometric_Metrics_3.C.

References edge_length(), p1, sqrt(), tet_vol(), tri_area(), and v.

Referenced by Aspect_Metric_3::getAspects().

                                                                             {

  // This metric is only defined for tetrahedrons
  if (_type == COM::Connectivity::TET4){

    // Use formulas from mathworld to find circumradius (R),
    // inradius (r), and shortest edge length (l)

    double a1 = tri_area(v[0],v[2],v[3]);
    double a2 = tri_area(v[0],v[4],v[6]);
    double a3 = tri_area(v[2],v[5],v[6]);
    double a4 = tri_area(v[3],v[4],v[5]);
    double a_sum = a1+a2+a3+a4;


    double len_a = edge_length(v[0]);
    double len_b = edge_length(v[2]);
    double len_c = edge_length(v[3]);
    double len_ap = edge_length(v[5]);
    double len_bp = edge_length(v[4]);
    double len_cp = edge_length(v[6]);

    double p1 = len_a * len_ap;
    double p2 = len_b * len_bp;
    double p3 = len_c * len_cp;
    double p_prod = sqrt((p1+p2+p3)*(p1+p2-p3)*(p1-p2+p3)*(p2+p3-p1));

    double vol = tet_vol(v[5],v[4],v[6]);

    R= p_prod/(24.0*vol);
    r = (3.0*vol)/a_sum;
    l = len_a;
    if( len_b < l ){ l = len_b;}
    if( len_c < l ){ l = len_c;}
    if( len_ap < l ){ l = len_ap;}
    if( len_bp < l ){ l = len_bp;}
    if( len_cp < l ){ l = len_cp;}
  }
  else{
    R = 1.0;
    r = 1.0;
    l = 1.0;
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

void initialize ( Vector_3< double >  n[], int  type  )

virtual

Initialize a 3D Geometric Metric by nodal coords and element type.

Parameters

n[]	Ordered set of nodal coordinates.
type	Element type: TET or HEX

Implements Metric.

Definition at line 47 of file Geometric_Metrics_3.C.

References v.

Referenced by Rocmop::add_aspect_ratios(), Rocmop::check_all_elem_quality(), Rocmop::check_marked_elem_quality(), main(), Rocmop::obtain_extremal_dihedrals(), Rocmop::perturb_stationary(), Rocmop::print_extremal_dihedrals(), Rocmop::print_mquality(), Rocmop::print_quality(), and Rocmop::smooth_vol_mesq_ng().

                                                                {
  _type = type;
  if (_type == COM::Connectivity::TET4){
    v.resize(7);
    v[0]= n[2]-n[1]; v[1]= n[1]-n[2]; v[2]= n[2]-n[0];
    v[3]= n[1]-n[0]; v[4]= n[3]-n[1]; v[5]= n[3]-n[0];
    v[6]= n[3]-n[2];
  }
  else if (_type == COM::Connectivity::HEX8){
    v.resize(8);
    v[0]= n[1]-n[0]; v[1]= n[3]-n[0]; v[2]= n[1]-n[2]; v[3]= n[3]-n[2]; 
    v[4]= n[5]-n[1]; v[5]= n[7]-n[3]; v[6]= n[5]-n[4]; v[7]= n[7]-n[4];
  }
}

Here is the caller graph for this function:

void initialize ( Element_node_enumerator &  ene )

virtual

Initialize a 3D Geometric Metric by Element_node_enumerator.

Parameters

ene	Element_node_enumerator

Implements Metric.

Definition at line 62 of file Geometric_Metrics_3.C.

References COM_assertion_msg, n, and v.

                                                              {
  _type = ene.type();
  if(ene.type() == COM::Connectivity::TET4){
    v.resize(7);
    const std::string nc("nc");
    Element_node_vectors_k_const<double> n;
    n.set(ene.pane()->attribute(nc),ene);
    v[0][0]=n(2,0)-n(1,0); v[0][1]=n(2,1)-n(1,1); v[0][2]=n(2,2)-n(1,2);
    v[1][0]=n(1,0)-n(2,0); v[1][1]=n(1,1)-n(2,1); v[1][2]=n(1,2)-n(2,2);    
    v[2][0]=n(2,0)-n(0,0); v[2][1]=n(2,1)-n(0,1); v[2][2]=n(2,2)-n(0,2);
    v[3][0]=n(1,0)-n(0,0); v[3][1]=n(1,1)-n(0,1); v[3][2]=n(1,2)-n(0,2);
    v[4][0]=n(3,0)-n(1,0); v[4][1]=n(3,1)-n(1,1); v[4][2]=n(3,2)-n(1,2);
    v[5][0]=n(3,0)-n(0,0); v[5][1]=n(3,1)-n(0,1); v[5][2]=n(3,2)-n(0,2);
    v[6][0]=n(3,0)-n(2,0); v[6][1]=n(3,1)-n(2,1); v[6][2]=n(3,2)-n(2,2);
  }
  else if (ene.type() == COM::Connectivity::HEX8){
    v.resize(8);
    const std::string nc("nc");
    Element_node_vectors_k_const<double> n;
    n.set(ene.pane()->attribute(nc),ene);
    v[0][0]=n(1,0)-n(0,0); v[0][1]=n(1,1)-n(0,1); v[0][2]=n(1,2)-n(0,2);
    v[1][0]=n(3,0)-n(0,0); v[1][1]=n(3,1)-n(0,1); v[1][2]=n(3,2)-n(0,2);    
    v[2][0]=n(1,0)-n(2,0); v[2][1]=n(1,1)-n(2,1); v[2][2]=n(1,2)-n(2,2);
    v[3][0]=n(3,0)-n(2,0); v[3][1]=n(3,1)-n(2,1); v[3][2]=n(3,2)-n(2,2);
    v[4][0]=n(5,0)-n(1,0); v[4][1]=n(5,1)-n(1,1); v[4][2]=n(5,2)-n(1,2);
    v[5][0]=n(7,0)-n(3,0); v[5][1]=n(7,1)-n(3,1); v[5][2]=n(7,2)-n(3,2);
    v[6][0]=n(5,0)-n(4,0); v[6][1]=n(5,1)-n(4,1); v[6][2]=n(5,2)-n(4,2);
    v[7][0]=n(7,0)-n(4,0); v[7][1]=n(7,1)-n(4,1); v[7][2]=n(7,2)-n(4,2);
  }
  else if (ene.type() == COM::Connectivity::PYRIMID5 ||
           ene.type() == COM::Connectivity::PRISM6){
    _type = ene.type();
    _ene_pane = ene.pane();
    _ene_i    = ene.id();
  }
  else COM_assertion_msg(0,"Element type not supported for 3D geometric metrics");
}

virtual double maxValue ( ) const

inlinevirtual

The maximum value for this metric.

Implements Metric.

Reimplemented in Aspect_Metric_3, and Angle_Metric_3.

Definition at line 66 of file Geometric_Metrics_3.h.

{ return 1.0; }

virtual double minValue ( ) const

inlinevirtual

The minimum value for this metric.

Implements Metric.

Reimplemented in Aspect_Metric_3, and Angle_Metric_3.

Definition at line 69 of file Geometric_Metrics_3.h.

{ return 0.0; }

Member Data Documentation

int _ene_i

protected

Definition at line 83 of file Geometric_Metrics_3.h.

const COM::Pane* _ene_pane

protected

Definition at line 82 of file Geometric_Metrics_3.h.

int _type

protected

Definition at line 81 of file Geometric_Metrics_3.h.

std::vector<Vector_3<double> > v

protected

Definition at line 80 of file Geometric_Metrics_3.h.

---

The documentation for this class was generated from the following files:

• Geometric_Metrics_3.h
• Geometric_Metrics_3.C